Предмет: Алгебра,
автор: iulllis
Решите пожалуйста уравнения через дискриминант, см вложение
Приложения:
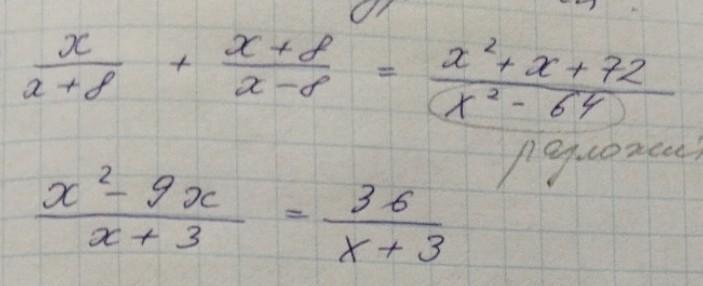
Ответы
Автор ответа:
1
1)
Область определения: x ≠ -8; x ≠ 8
Умножаем уравнение на (x-8)(x+8). Избавляемся от дробей.
x(x-8) + (x+8)(x+8) = x^2 + x + 72
x^2 - 8x + x^2 + 16x + 64 = x^2 + x + 72
x^2 + 7x - 8 = 0
Решаем через дискриминант, хотя по теореме Виета проще.
D = 7^2 - 4*1(-8) = 49 + 32 = 81 = 9^2
x1 = (-7 - 9)/2 = -16/2 = -8 - не входит в область определения.
x2 = (-7 + 9)/2 = 2/2 = 1
Ответ: x = 1
2)
Область определения: x ≠ -3
Умножаем уравнение на (x+3)
x^2 - 9x = 36
x^2 - 9x - 36 = 0
D = (-9)^2 - 4*1(-36) = 81 + 144 = 225 = 15^2
x1 = (9 - 15)/2 = -6/2 = -3 - не входит в область определения
x2 = (9 + 15)/2 = 24/2 = 12
Ответ: x = 12
Похожие вопросы
Предмет: Русский язык,
автор: lilka9
Предмет: Русский язык,
автор: helenvaganova
Предмет: Окружающий мир,
автор: богдан255
Предмет: Химия,
автор: DinaVay007
Предмет: Другие предметы,
автор: prens444