СРОЧНО ПОМОГИТЕ ДАЮ 50 БАЛЛОВ

Ответы
Ответ:
6√6 см ≈ 14,7 см.
Объяснение:
Если в условии требуется найти диагональ параллелограмма, делящую один из его углов на углы, равные 45° и 75°, то решение приведено ниже.
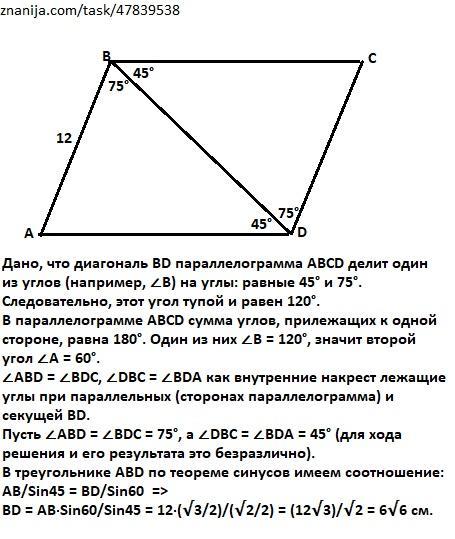
Дано, что диагональ BD параллелограмма ABCD делит один из углов (например, ∠В) на углы: равные 45° и 75°. Следовательно, этот угол тупой и равен 120°.
В параллелограмме АВСD сумма углов, прилежащих к одной стороне, равна 180°. Один из них ∠В = 120°, значит второй угол ∠А = 60°.
∠ABD = ∠BDC, ∠DBC = ∠BDA как внутренние накрест лежащие углы при параллельных (сторонах параллелограмма) и секущей BD.
Пусть ∠ABD = ∠BDC = 75°, а ∠DBC = ∠BDA = 45° (для хода решения и его результата это безразлично).
В треугольнике АВD по теореме синусов имеем соотношение:
АВ/Sin45 = BD/Sin60 =>
BD = AB·Sin60/Sin45 = 12·(√3/2)/(√2/2) = (12√3)/√2 = 6√6 см.
P.S. Если требуется найти и вторую диагональ, то далее по теореме синусов надо найти вторую сторону параллелограмма:
AD/Sin75 = АВ/Sin45 =>
AD = AB·Sin75/Sin45.
Sin75 = Sin(30+45) = Sin30·cos45+cos30·sin45 = (√2+√6)/4.
AD = 12·((√2+√6)/4)/(√2/2) = (12√3)/√2 = 6(1+√3) см.
ВС = АD = 6(1+√3) см.
И теперь по теореме косинусов можно найти и вторую диагональ (пожалуйста, поупражняйтесь сами...)