Предмет: Алгебра,
автор: dan1942
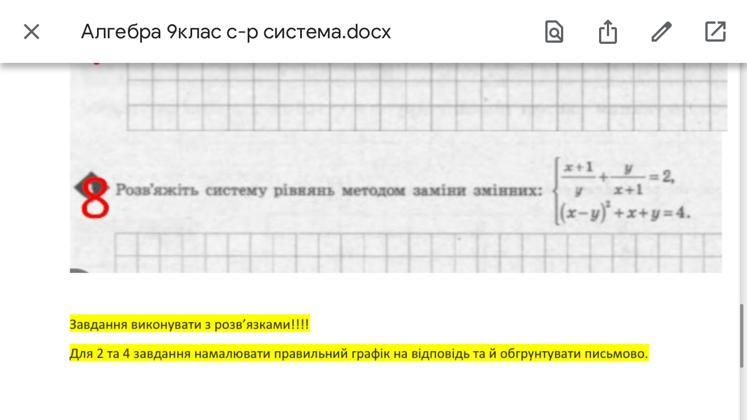
розв'яжіть систему рівнянь методом заміни змінних
Приложения:
Ответы
Автор ответа:
2
Объяснение:
Рассмотрим первое уравнение:
Пусть
Подставляем у=х+1 во второе уравнение:
Ответ: (1;2).
kakoytokirya:
ПОМОГИТЕ МНЕ ТОЖЕ, УМОЛЯЮ, В МОЕМ ПРОФИЛЕ ОДИН ВОПРОС, ПРОШУ, У МЕНЯ СОР
ПОЖАЛУЙСТА
Похожие вопросы
Предмет: Українська мова,
автор: яяяя136
Предмет: Другие предметы,
автор: JTXLive
Предмет: Английский язык,
автор: ddlovat
Предмет: Немецкий язык,
автор: nikolayizyumov