Предмет: Геометрия,
автор: novruzovilkin847
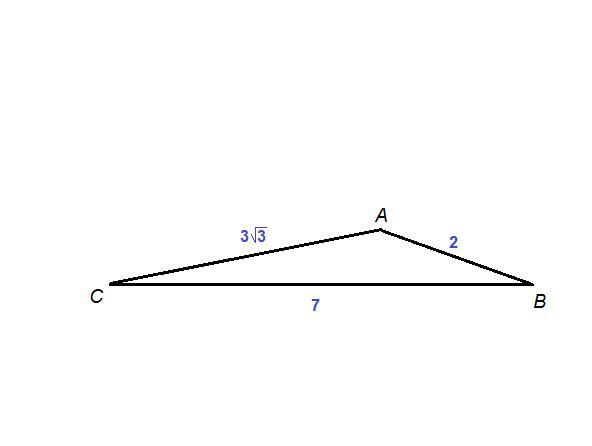
Стороны треугольника ABC : AB=2см, AC=3/3 , ВС=7см. Найдите наибольший угол треугольника ABC.
Дайте нормальные ответы пожалуйста!
ismanagi:
Есть решение этого задания ?
Что значит АС = 3/3?
Ответы
Автор ответа:
9
Ответ:
Больший угол равен 120°.
Объяснение:
ΔАВС,
АВ = 2 см, АС = 3√3 см, ВС = 7 см
В треугольнике больший угол лежит против большей стороны.
ВС = 7 см - большая сторона, значит ∠А - больший.
Теорема косинусов:
- квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.
BC² = AC² + AB² - 2 · AC · AB · cos∠A
7² = (3√3)² + 2² - 2 · 3√3 · 2 · cos∠A
49 = 27 + 4 - 12√3 · cos∠A
12√3 · cos∠A = 31 - 49
∠A = 120°
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: skilletsk
Предмет: Английский язык,
автор: Павлендий
Предмет: Русский язык,
автор: chystrik
Предмет: Информатика,
автор: cocoma2303
Предмет: Литература,
автор: tursunbaevamaira