Предмет: Геометрия,
автор: dima28188331
Точку на стороне параллело- грамма соединили с его противоположными вершинами. Какую часть площади параллелограмма составляет полученный треугольник?
Ответы
Автор ответа:
4
Ответ:
Объяснение:
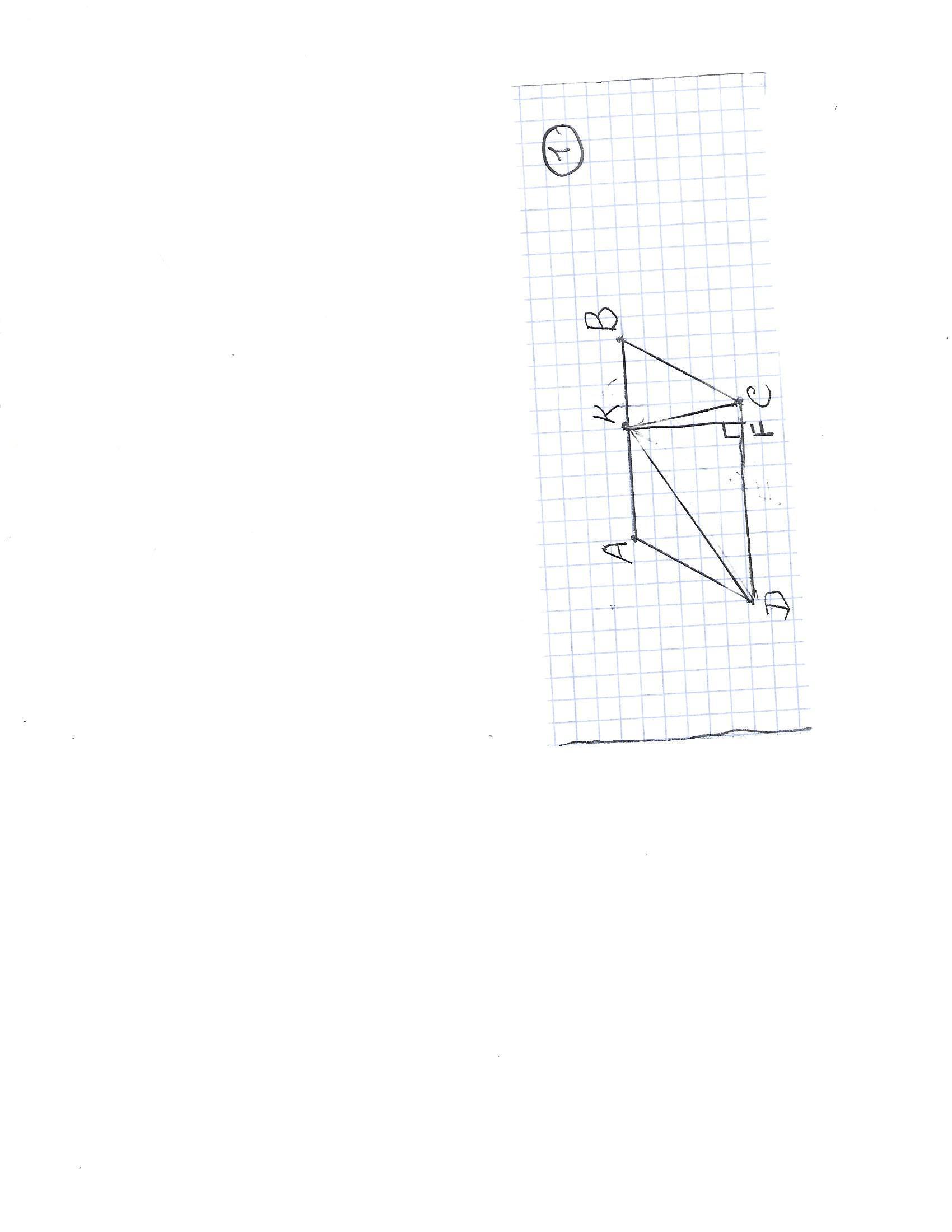
Параллелограмм АВСD и точка К на стороне АВ. Опустим из точки К перпендикуляр на сторону DС. Это высота,как в треугольнике,так и в параллелограмме. Находим площадь треугольника
Теперь напишем формулу площади параллелограмма АВСD
и найдем отношение площади треугольника к площади параллелограмма. Отношение 1:2
Площадь треугольника составляет половину(1/2) площади параллелограмма.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: ник2878
Предмет: Русский язык,
автор: vazgecgonlum
Предмет: Русский язык,
автор: taniazhtltbkovf
Предмет: Русский язык,
автор: lailuka
Предмет: Право,
автор: tsirillla