Предмет: Геометрия,
автор: potatoshkagm
ПОМОГИТЕ ПОЖАЛУЙСТА, НУЖНО РЕШИТЬ КАК ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
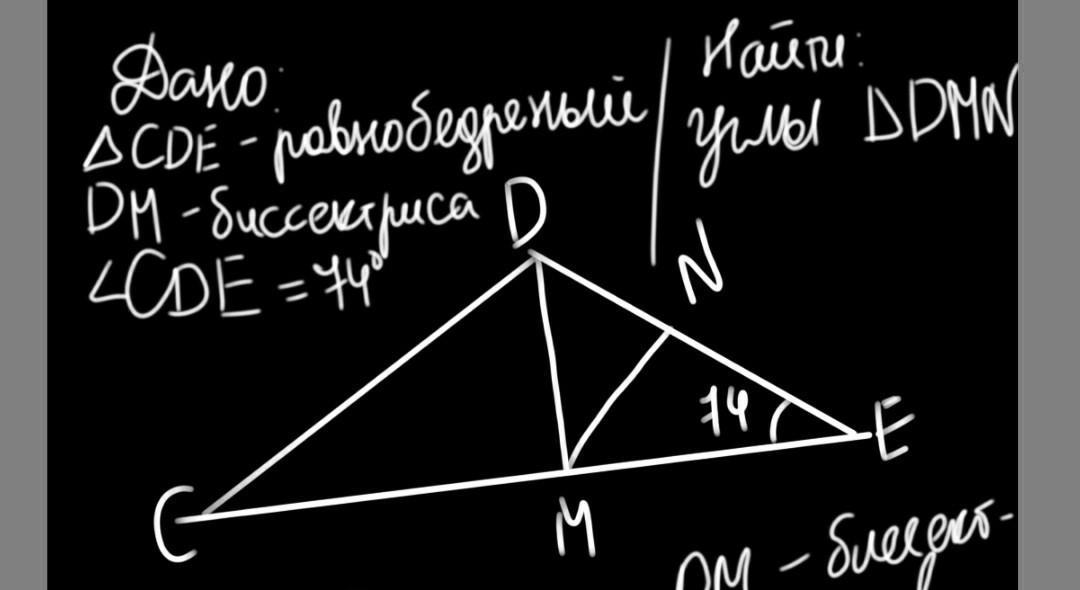
Отрезок DM - биссектриса треугольника CDE. Через точку M проведена прямая пересекающая сторону DE в точке N. DN = MN Найти углы треугольника DMN если угол CDE = 74 градуса.
Ответы
Автор ответа:
1
Там рисунок, перерисуешь в тетрадь.
Поскольку отрезок DM - биссектриса ∆CDE, то она выступает в роли медианы и высоту, а значит делит треугольник ещё на 2∆, то есть CDM и DME.
Далее, ∆DME получается имеет также биссектрису(которая как и медиана, так и высота) NM на ещё 2∆(прямоугольных) = DMN и NEM. Тогда DMN=NEM (за III признаком сходства). Соответственно, угол D= углу Е = 74°.
Угол N у обоих треугольников 90°.
Знаем, что в в прямоугольном треугольнике сумма всех углов равно 180°. Отсюда, угол D и N известны. Тогда, E = 180°-(90+74)= 16°. Аналогично у ∆NME.
Итог: Угол D = 74,
N = 90,
E = 16.
В принципе все, так и решается
Приложения:
potatoshkagm:
мы не проходили сумму углов треугольника, поэтому это неправильное решение
Всмысле неправильно? Решение правильное. У любого треугольника(прямоугольный, равносторонний, равнобедренный) всегда сумма всех углов 180°. Равенства может не проходили, а сумма углов всегда одинаковая. По этому, если вы не проходили данный материал, это ещё не говорит о том, что решение не правильное
Единственное, я нашла углы ∆DNE, a надо ∆DMN. Но там суть не меняется, потому что 3й признак сходства гласит: «Если все стороны и углы одного треугольника одинаково равны другому треугольнику, то такие треугольники равны(одинаковые)».
Просто писала ночью((
извините, неправильно сформулировала, решение и правда правильное, но нам нельзя использовать правило, что углы треугольников 180°, поэтому ваше решение мне не помогло
Хорошо. А каким решением вы пользуетесь? Подобные задания делали?
я не в курсе, я болела, по-моему, мы такое не решали
мне кажется, здесь должно быть доп. построение, но я не знаю куда
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: aiana228
Предмет: Английский язык,
автор: eldenizkazimov
Предмет: Математика,
автор: gagy54
Предмет: Алгебра,
автор: Ksushasheoa