Question

Помогите
33 балла пожалуйста

Answer 1

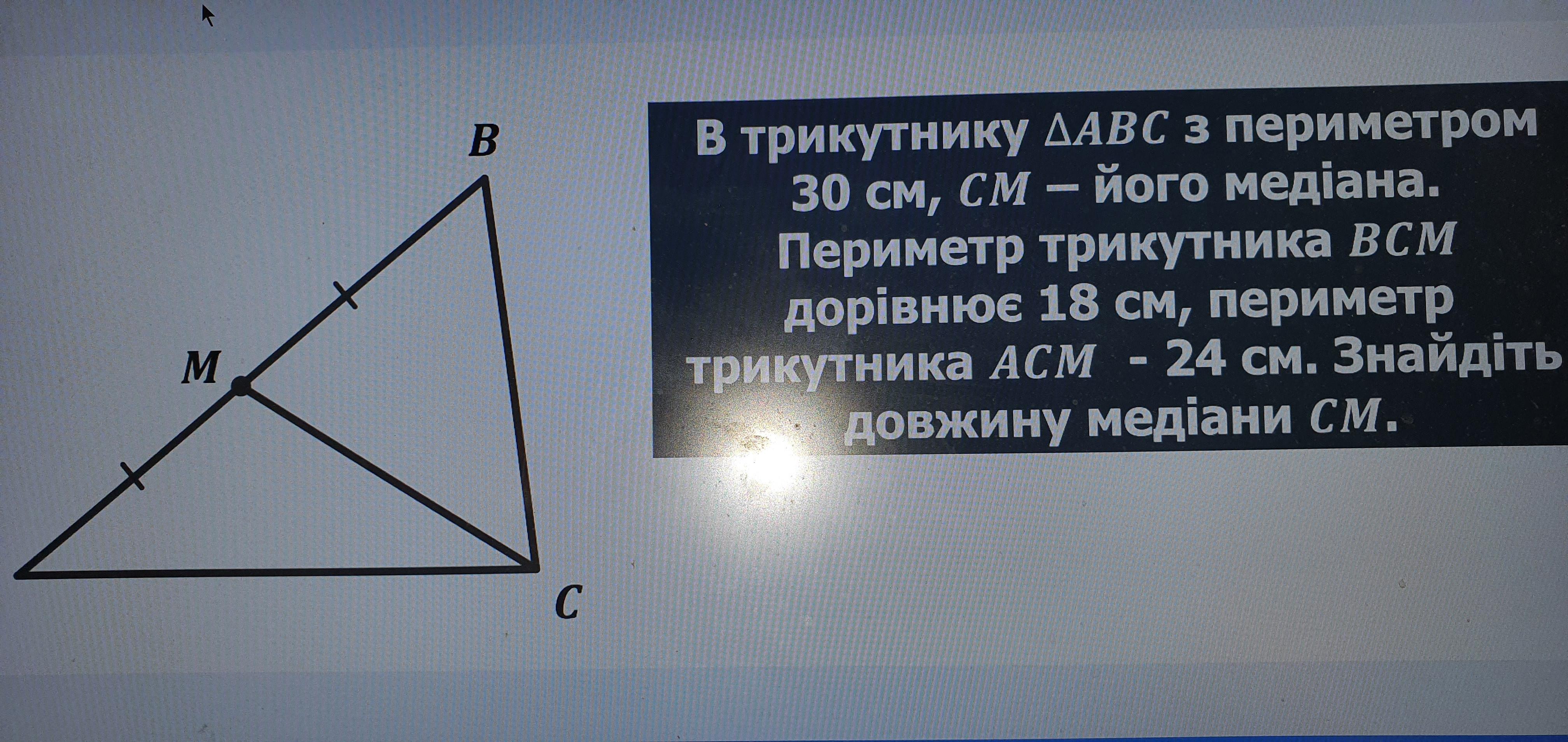
Примем длину медианы СМ = х, а половины стороны АВ - у.

Запишем условия задачи.

Р(BCM) = x + y + BC = 18,

Р(ACM) = x + y + AC = 24.

Отсюда видно, что сторона АС на 6 см больше, то есть:

АС = ВС + 6.

Используем периметры для определения сторон.

ВС = 18 - х - y,

АС = 24 - х - у.

Периметр АВС: 30 = 2у + 18 - х - у + 24 - х - у = 42 - 2х.

Отсюда находим длину медианы: СМ = х = (42 - 30)/2 = 6 см.

Зная длину медианы, можно определить длины сторон по формуле:

4СМ² = 2a² + 2b² - c².

Подставим b = a + 6, c = 30 - a - b = 30 - a - a - 6 = 24 - 2a.

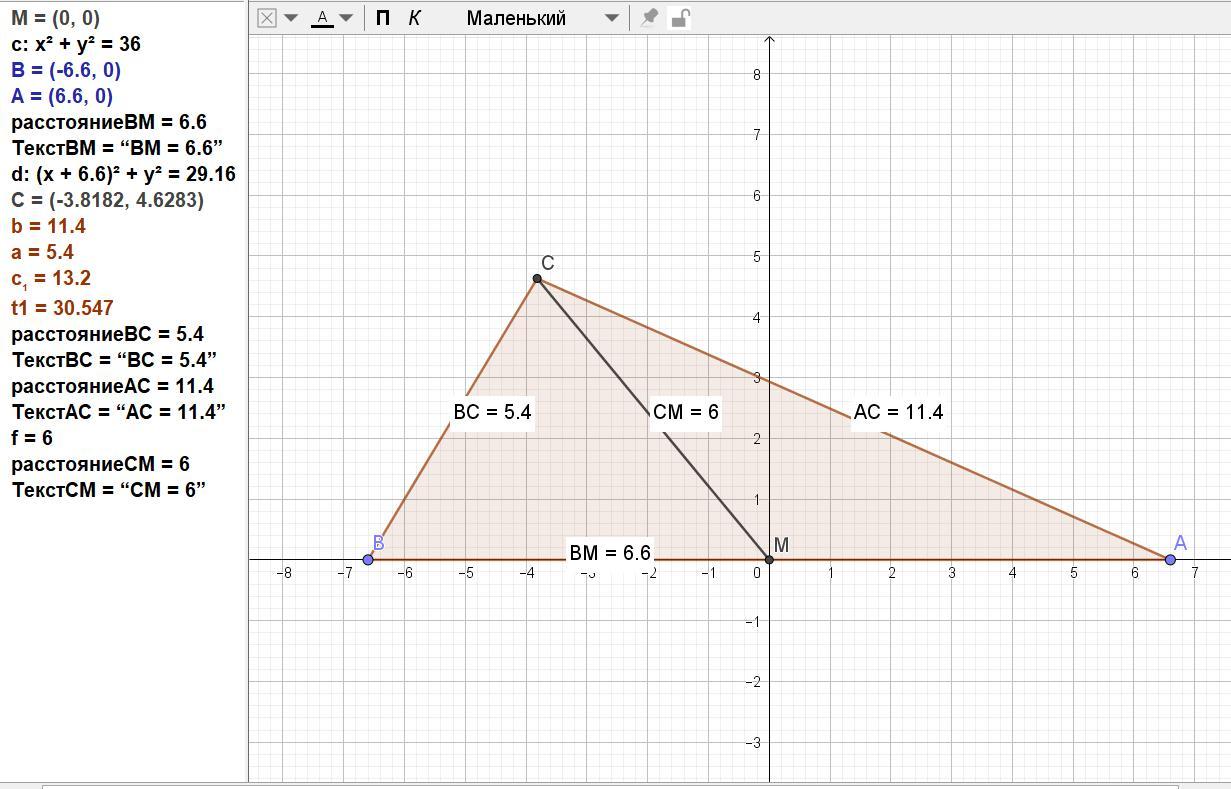
Подставив в формулу, получаем а = 5,4 см, b = 11,4, c = 13,2 см.