Question

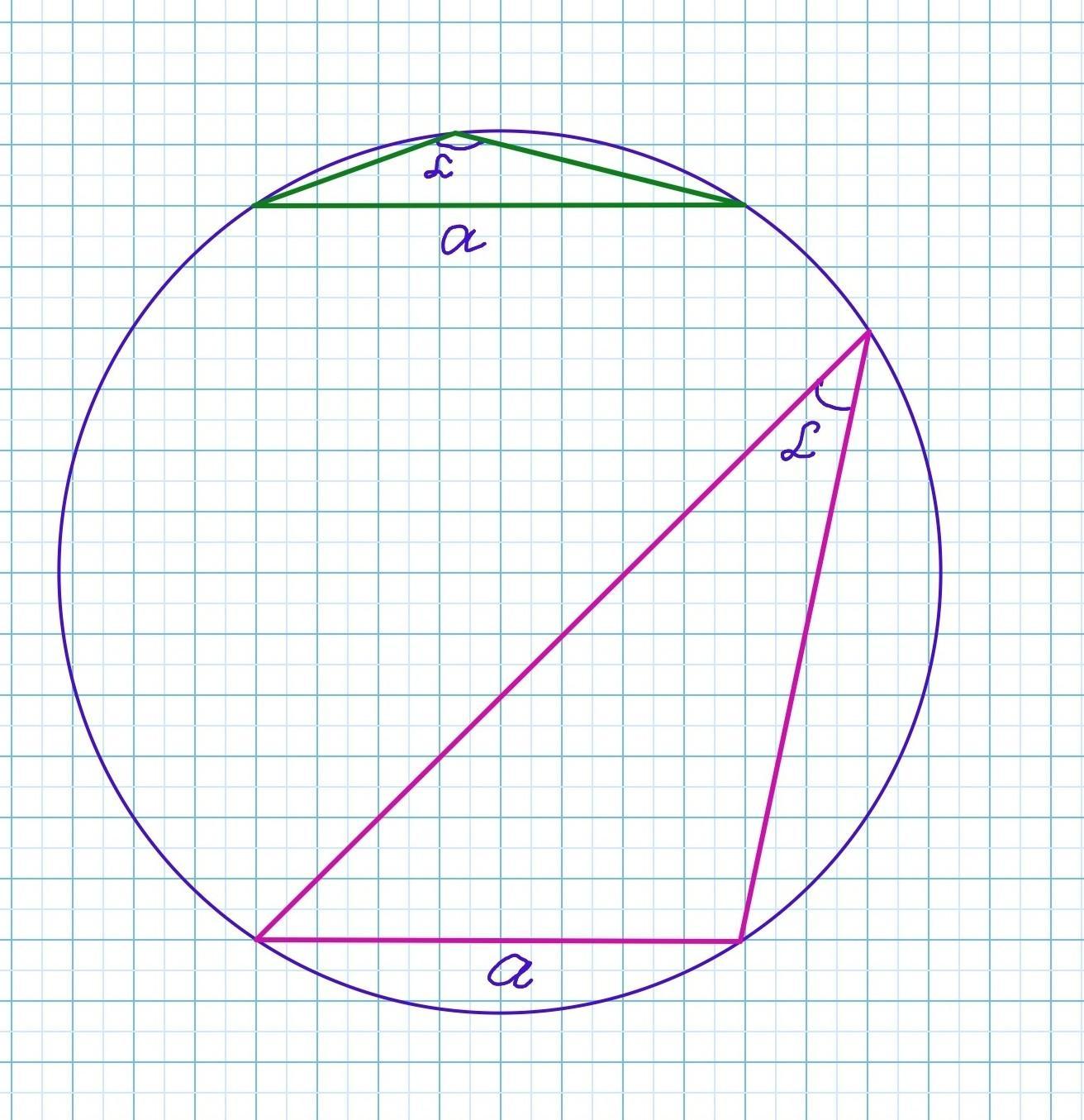
Одна из сторон треугольника равна радиусу описанной окружности. Найдите угол, противолежащий этой стороне. Обратите внимание на необходимость рассмотрения 2 случаев(А-острый угол и А-тупой угол).
Можно пожалуйста с решением. В ответе должно получиться 30° и 150°.​

Answer 1

Ответ:

30°, 150°

Объяснение:

По теореме синусов:

$\dfrac{a}{ \sin\alpha } = 2R$

а- сторона, противолежащая углу α

R - радиус описанной вокруг треугольника окружности.

По условию задачи а = R.

$\sin \alpha = \dfrac{a}{2R} = \dfrac{R}{2R} = \dfrac{1}{2}$

sin α = sin (180°- α) - согласно формулами приведения. Угол α может быть тупым или острым.

∠α = 30° либо ∠α = 150°