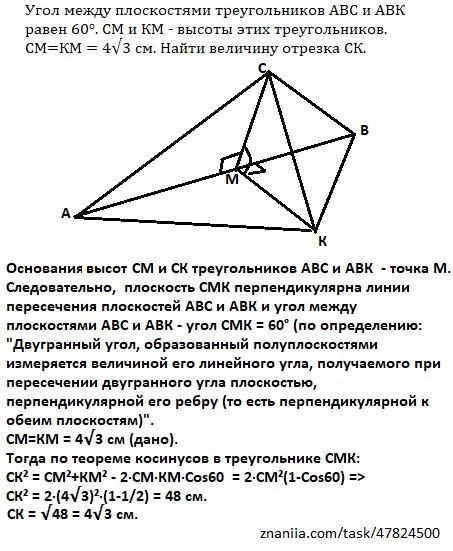
кут між площинами трикутників АВС і АВК дорівнює 60°.СМ і КМ висоти цих трикутників. СМ=КМ = 4√3.см. Знайти довжину відрізка СК.
Ответы
Ответ:
СК = 4√3 см.
Объяснение:
Основания высот СМ и СК треугольников АВС и АВК - точка М. Следовательно, плоскость СМК перпендикулярна линии пересечения плоскостей АВС и АВК и угол между плоскостями АВС и АВК - угол СМК = 60° (по определению: "Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру (то есть перпендикулярной к обеим плоскостям)".
В треугольнике СМК СМ=КМ (дано), а угол при вершине ∠М= 60°. Следовательно, треугольник СМК - правильный и СК = СМ = КМ = 4√3 см.
Или так:
СМ=КМ = 4√3 см (дано).
Тогда по теореме косинусов в треугольнике СМК:
СК² = СМ²+КМ² - 2·СМ·КМ·Сos60 = 2·СМ²(1-Сos60) =>
СК² = 2·(4√3)²·(1-1/2) = 48 см.
СК = √48 = 4√3 см.