Предмет: Математика,
автор: valeskaforever12
Решите уровнение
1) 3cos^2x+7sinx-5=0
2) 2sin^2x+1,5sin2x-3cos^2x=1
Ответы
Автор ответа:
0
Решение:
1)
3cos²x + 7sinx - 5 = 0
3(1 - sin²x) + 7sinx - 5 = 0
3 - 3sin²x + 7sinx - 5 = 0
3sin²x - 7sinx + 2 = 0
sinx = t
3t² - 7t + 2 = 0
D = 49 - 24 = 25
t₁ = (7 - 5) / 6 = 1/3 t₂ = (7 + 5) / 6 = 2
sinx = 1/3 sinx = 2 - нет корней
x = (- 1)ⁿ· arcsin (1/3) + πn, n∈Z
2)
2 * sin² x + 1.5 * sin (2 * x) - 3 * cos² x = 1
2 * sin² x + 3 * sin x * cos x - 3 * cos² x = sin² x + cos² x
Разделим на cos² x
2 * tg² x + 3 * tg x - 3 = tg² x + 1
tg² x + 3 * tg x - 4 = 0
Обозначим tg x =t
t² + 3t - 4 = 0
По теореме Виета:
t1 * t2= -4
t1+ t2 = -3
t1 =-4
t2= 1
Значит
tg x = -4, откуда x = arctg (-4) + pi * k;
tg x= 1, откуда х = pi/4 + pi * k.
Автор ответа:
0
Ответ:
Ответ на фото))))
Пошаговое объяснение:
Приложения:
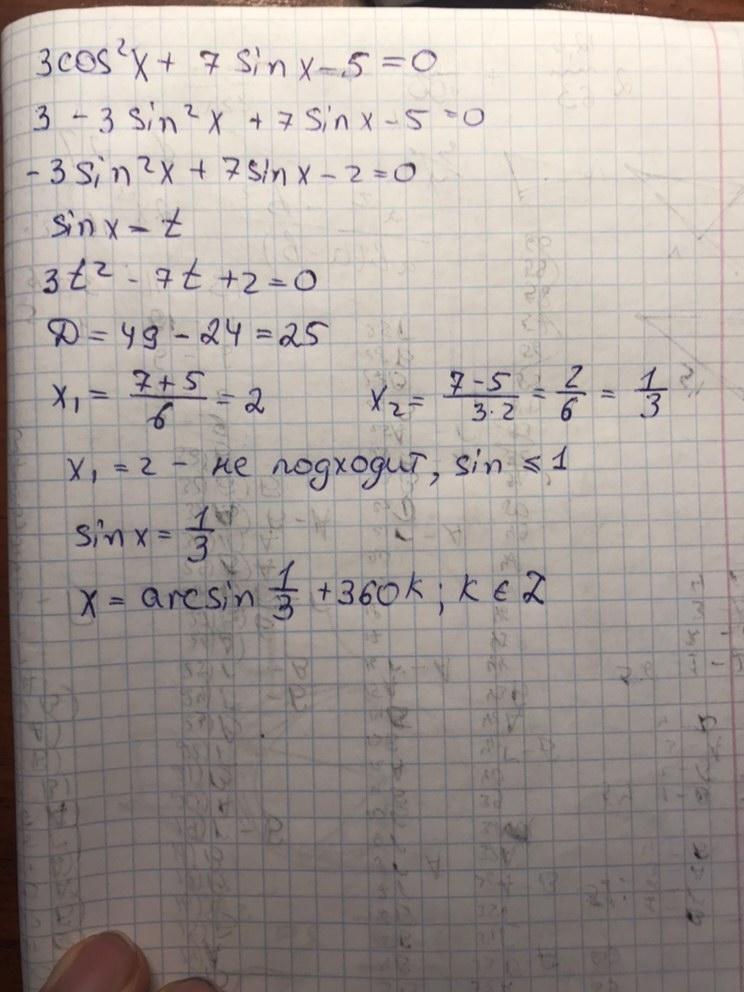

Похожие вопросы
Предмет: Русский язык,
автор: ilya31ru
Предмет: Русский язык,
автор: kilida22
Предмет: Русский язык,
автор: hikmetnebiyev
Предмет: История,
автор: angelinamikhay
Предмет: Русский язык,
автор: Аноним