Предмет: Алгебра,
автор: kanalena04
Помогите решить 84 номер!
Приложения:
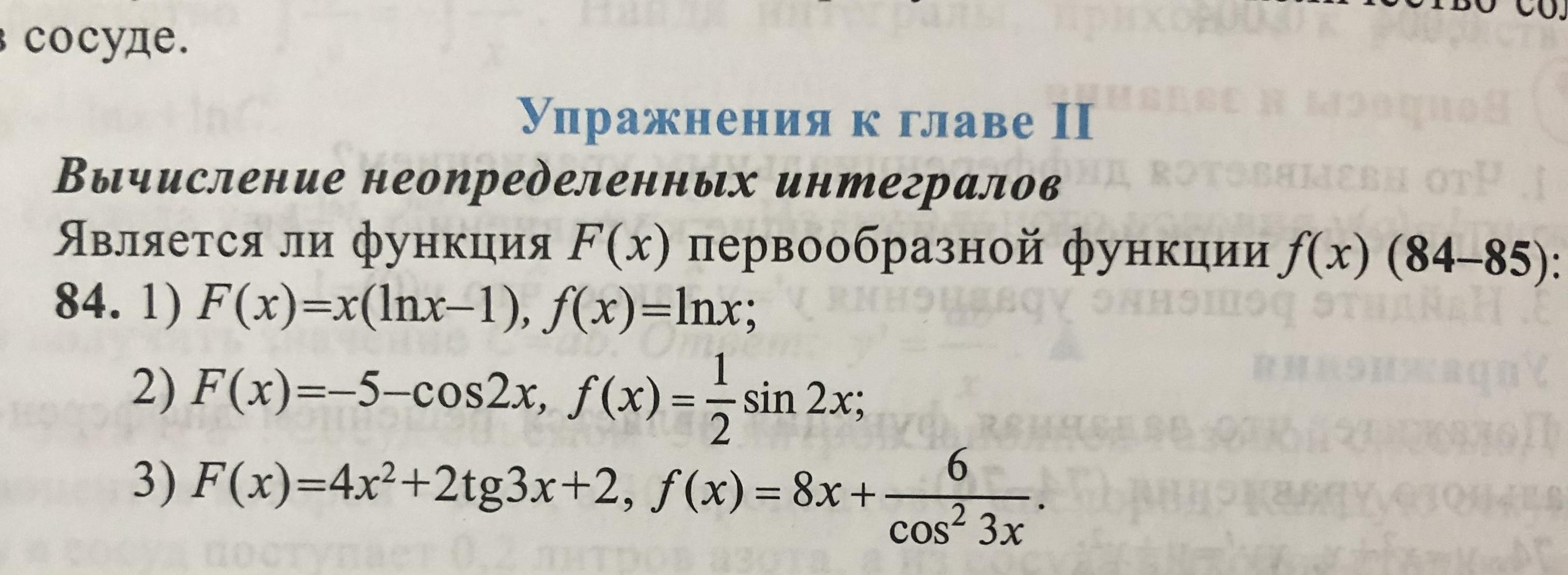
Ответы
Автор ответа:
0
Ответ:
1) Да, 2) Нет, 3) Да
Объяснение:
Чтобы проверить, является ли F(x) первообразной для f(x), нужно взять производную F'(x) и сравнить её с f(x).
1) F(x) = x(ln x - 1); f(x) = ln x
F'(x) = 1(ln x - 1) + x*1/x = ln x - 1 + 1 = ln x = f(x)
Да, F(x) - первообразная для f(x)
2) F(x) = -5 - cos (2x); f(x) = 1/2*sin (2x)
F'(x) = - (-sin (2x))*2 = 2sin (2x) ≠ f(x)
Нет, F(x) не является первообразной для f(x).
3) F(x) = 4x^2 + 2tg (3x) + 2;
Да, F(x) - первообразная для f(x)
Похожие вопросы
Предмет: Русский язык,
автор: лиса188
Предмет: Русский язык,
автор: asrtffcvv
Предмет: Русский язык,
автор: Мелексима
Предмет: Қазақ тiлi,
автор: двнил7574
Предмет: История,
автор: jfhshbh