Предмет: Алгебра,
автор: Simba2017
Дифференциальные вычисления
Приложения:
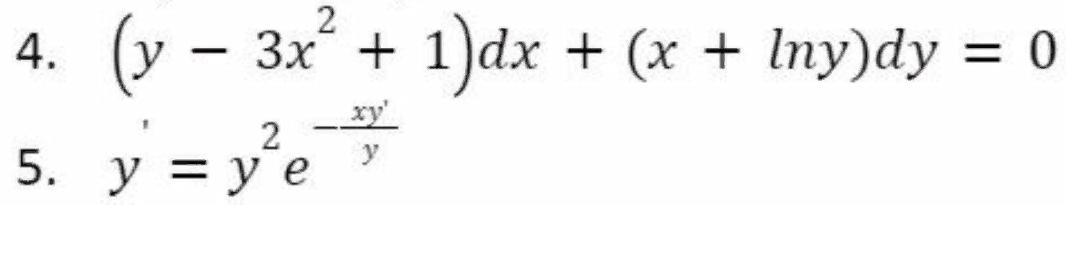
Ответы
Автор ответа:
2
4) Заметим, что это уравнение в полных дифференциалах. И правда:
Тогда решение данного ДУ можно записать в виде . При этом
Определяем неизвестную функцию:
Окончательно
5) Замена :
- получено уравнение Лагранжа.
Полагаем , дифференцируем по
:
1.
Подставим в исходное ДУ:
2. Проверим особое решение:
Подставим в исходное ДУ:
Окончательно
Simba2017:
спасибо вам!
Похожие вопросы
Предмет: Русский язык,
автор: darya201317
Предмет: Русский язык,
автор: nikitavlasov123
Предмет: Английский язык,
автор: elya2205
Предмет: Математика,
автор: mopsag79
Предмет: Математика,
автор: 0512ь