Предмет: Алгебра,
автор: olesechka2004
Вычислите пожалуйста интеграл(пункты 2,4,6)
Приложения:
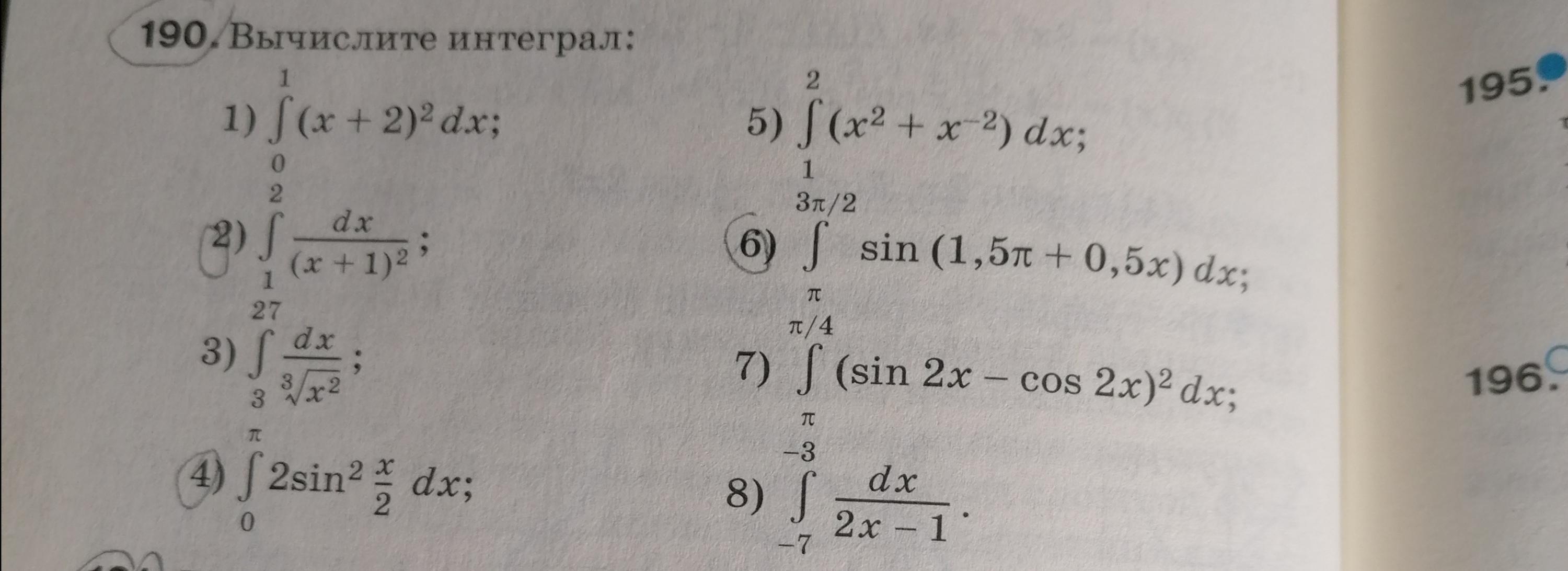
Ответы
Автор ответа:
1
Ответ: 2) 5/36; 4) π; 6) 2-√2.
Объяснение:
2)обозначим искомый интеграл через I. По формуле Ньютона-Лейбница, I=F(2)-F(1), где F(x) - первообразная для функции f(x)=1/(x+1)².
F(x)=∫f(x)*dx=∫dx/(x+1)²=∫d(x+1)/(x+1)²=-1/(x+1)+C, где C - произвольная постоянная. Отсюда I=-1/(2+1)²+C-(-1/(1+1)²+C)=-1/9+1/4=5/36.
4) I=F(π)-F(0), F(x)=∫2*sin²(x/2)*dx. Так как sin²(x/2)=(1-cos(x))/2, то ∫2*sin²(x/2)*dx=∫[1-cos(x)]*dx=∫dx-∫cos(x)*dx=x-sin(x)+C. Отсюда I=π-sin(π)-[0-sin(0)]=π.
6) I=F(3*π/2)-F(π), F(x)=∫sin(3*π/2+x/2)*dx. Так как sin(3*π/2+x/2)=-cos(x/2), то F(x)=-∫cos(x/2)*dx=-2*∫cos(x/2)*d(x/2)=-2*sin(x/2)+C. Отсюда I=-2*sin(3*π/4)+C-[-2*sin(π/2)+C]=-2*√2/2+2*1=2-√2.
Похожие вопросы
Предмет: Английский язык,
автор: yulechkaemelya
Предмет: Русский язык,
автор: Snejana17
Предмет: Қазақ тiлi,
автор: Азри
Предмет: Русский язык,
автор: sarrradaserty75379
Предмет: География,
автор: ВладиславДмитриевич4