Question

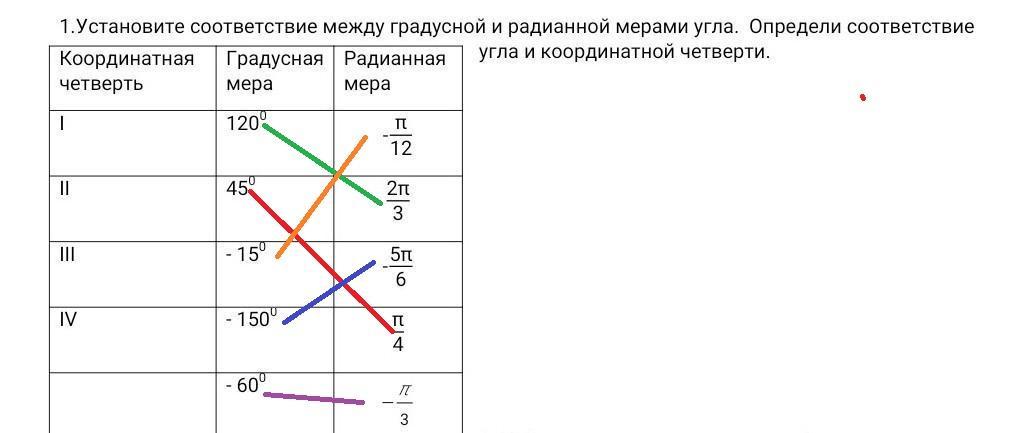
Установите соответствие между градусной и радианной мерами угла. Определи соответствие угла и координатной четверти. Координатная четверть Градусная мера Радианная мера I 1200 -π/12 II 450 2π/3 III - 150 -5π/6 IV - 1500 π/4 - 600 ​

Answer 1

Ответ:

на рисунках во вложении.

Пошаговое объяснение:

Установить соответствие между градусной и радианными мерами угла и определить координатные четверти.

Полное условие задания во вложении.

Чтобы установить связь между градусами и радианами, необходимо узнать градусную и радианную меру какого-либо угла.

Связь между радианами и градусами выражается формулой  π  радиан  = 180 °, соответственно

$\displaystyle 1\ rad =(\frac{180}{\pi })^{\circ}$

Также можно выразить один градус в радианах:

$\displaystyle 1^{\circ}=(\frac{\pi }{180})\ rad$

Формула перевода из градусов в радианы:

$\displaystyle x ^{\circ}=\frac{x^{\circ}*\pi }{180}\ rad$

Переведем градусные меры угла в радианы :

$\displaystyle 120 ^{\circ}=\frac{120*\pi }{180}=\frac{12\pi }{18}=\frac{2\pi }{3} \ rad$

$\displaystyle 45 ^{\circ}=\frac{45*\pi }{180}=\frac{\pi }{4} \ rad$

$\displaystyle -15 ^{\circ}=\frac{-15*\pi }{180}=-\frac{\pi }{12} \ rad$

$\displaystyle -150 ^{\circ}=\frac{-150*\pi }{180}=-\frac{5\pi }{6} \ rad$

$\displaystyle -60 ^{\circ}=\frac{-60*\pi }{180}=-\frac{\pi }{3} \ rad$

Отметим соответствие в таблице ( рис. 2  во вложении)

Определим соответствие угла и координатной четверти.

Используем  шкалу:

α ∈ (0°; 90°) ⇒ это угол I координатной четверти;

α ∈ (90°; 180°) ⇒ II координатная четверть;

α ∈ (180°; 270°) ⇒ III координатная четверть;

α ∈ (270°; 360°) ⇒ IV координатная четверть.

Но у нас есть углы с отрицательной градусной мерой.

Для того , чтоб определить в какой координатной четверти находятся углы с отрицательной градусной мерой , надо найти соответствующий им положительный угол.

Для этого к отрицательному углу прибавляем 360° и   получим соответствующий  ему положительный угол.

-15° = 360 + (-15) = 345°

-150° = 360 + ( - 150) = 360 - 150 =210 °

- 60° = 360 + ( - 60) = 300°

Найдем в каких четвертях находятся наши углы :

120° - II координатная четверть;

45°  - I координатная четверть;

-15 = 345 - IV координатная четверть;

-150 = 210 - III координатная четверть;

-60 = 300  - IV координатная четверть.

Отметим это в таблице ( рис. 3 во вложении)