!!!РЕШИТЕ ПОЖАЛУЙСТА ООЧЕНЬ НАДО!!!
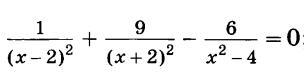
Ответы
Сразу установим значения, которые не будут являться корнями уравнения, так как обращают знаменатель хотя бы одной из дробей в 0.
Теперь, если в решении вылезет одно из этих двух значений, мы будем знать, что на самом деле это не корень уравнения. Теперь вернёмся к самому уравнению. Разложим разность квадратов в знаменателе третьего слагаемого.
Немного преобразуем дроби.
Переместим слагаемые местами.
Получаем ничто иное, как формулу квадрата разности!
В нашем уравнении по этой формуле получаем:
Приводим дроби к общему знаменателю.
Дробь равна нулю, когда числитель равен нулю, а знаменатель отличен от нуля. Ситуацию в знаменателе мы уже разбирали в начале решения, поэтому просто приравниваем числитель к нулю.
Это значение не выходит из области определения, а значит, корнем уравнения является.
Ответ: 4.