Question

Можно решение пожалуйста)

Answer 1

Здравствуй viktoriamartynova120!

В равнобедренном треугольнике ABC сторона АС - основание, ∟BCA=40°, ∟ABC = 100 °, BD - медиана. Найдите углы треугольника ABD.

Дано:

ABC - равнобедренный треугольник

AC - основание

∟BCA=40°

∟ABC = 100 °

BD - медиана

Найти углы треугольника ABD

Решение:

ΔАВС - равнобедренный, АС - основание, BD - медиана, проведенная к основанию.

По свойству равнобедренного треугольника ∟ВАС = ∟BCA = 40 °.

BD является  медианой, высотой, биссектрисой.

Под значением биссектрисы угла имеем:  

∟ABD = ∟CBD = ∟АВС : 2 ;

∟ABD = 50 °.

По определению высоты треугольника имеем:  

BD ┴ AC, ∟BDA = 90 °.

Ответ: 40 °, 50 °, 90 °.

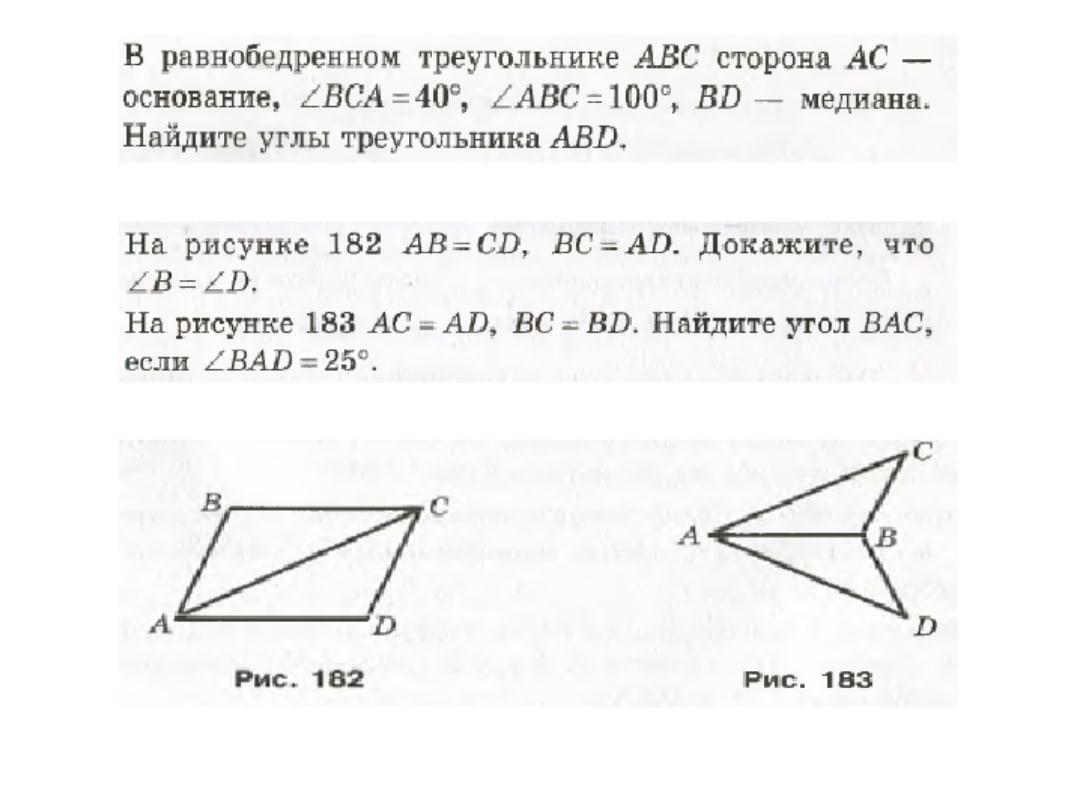
На рисунке 182 АВ = CD, ВС = AD. Докажите, что ∟B = ∟D

Дано:

АВ = CD

ВС = AD

Доказать:

∟B = ∟D

Доказательство:

Посмотрев на рисунок, мы можем выразить два треугольника, это ABC и ADC

1)АВ=CD (по условию)

2)BC=DA (по условию)

3)АС - общая сторона (по рисунку)  

Эти два треугольника равны по третьему признаку равенства треугольников. И из этого следует, что ∠B=∠D как соответственные стороны равных треугольников. Ч.т.д

На рисунке 183 АС = АD, BC = BD. Найдите угол ВАС, если ∟BAD = 25 °

Дано:

ΔDBA и ΔCBA

АС = АD

BC = BD

∟BAD = 25 °

Найти:

∠BAC

Решение:

Рассмотрим ΔDBA и ΔCBA

1) АС = AD (по условию)

2) ВС = BD (по условию)

3) AB - общая сторона

Треугольники равны по 3 признаку равенства треугольников.

Тогда, ∟BAC = ∟BAD = 25 °

Ответ: 25 °.

Удачи в дальнейших решениях!