Меньшее основание равнобедренной трапеции равно 12 см. Центр окружности, описанной
около трапеции, находится на большем основании, и её радиус равен 10 см. Найди
боковую сторону трапеции
Ответы
Ответ:
4√5 см .
Объяснение:
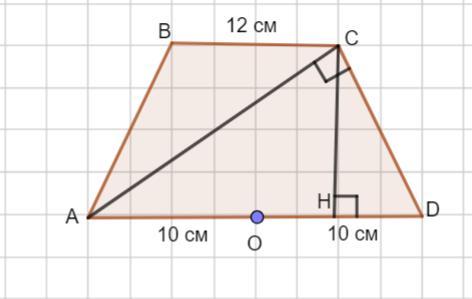
Пусть дана равнобедренная трапеция ABCD. Если центр описанной около трапеции окружности находится на большем основании, то это будет точка О - середина основания AD. Тогда большее основание AD=10+10=20 см.
Δ AСD - прямоугольный, так как AD - диаметр окружности, а вписанный угол, опирающийся на диаметр прямой.
Проведем высоту СН и трапеции и прямоугольного треугольника.
Если трапеция равнобедренная, то НD=(20-12):2=8:2=4 см.
Тогда АН= 20-4=16 см.
Так как высота прямоугольного треугольника, проведенная к гипотенузе есть среднее геометрическое отрезков, на которые делится гипотенуза высотой, то
CH= 8 см.
Рассмотрим ΔCHD - прямоугольный. Найдем CD по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Тогда боковая сторона трапеции равна 4√5 см