Question

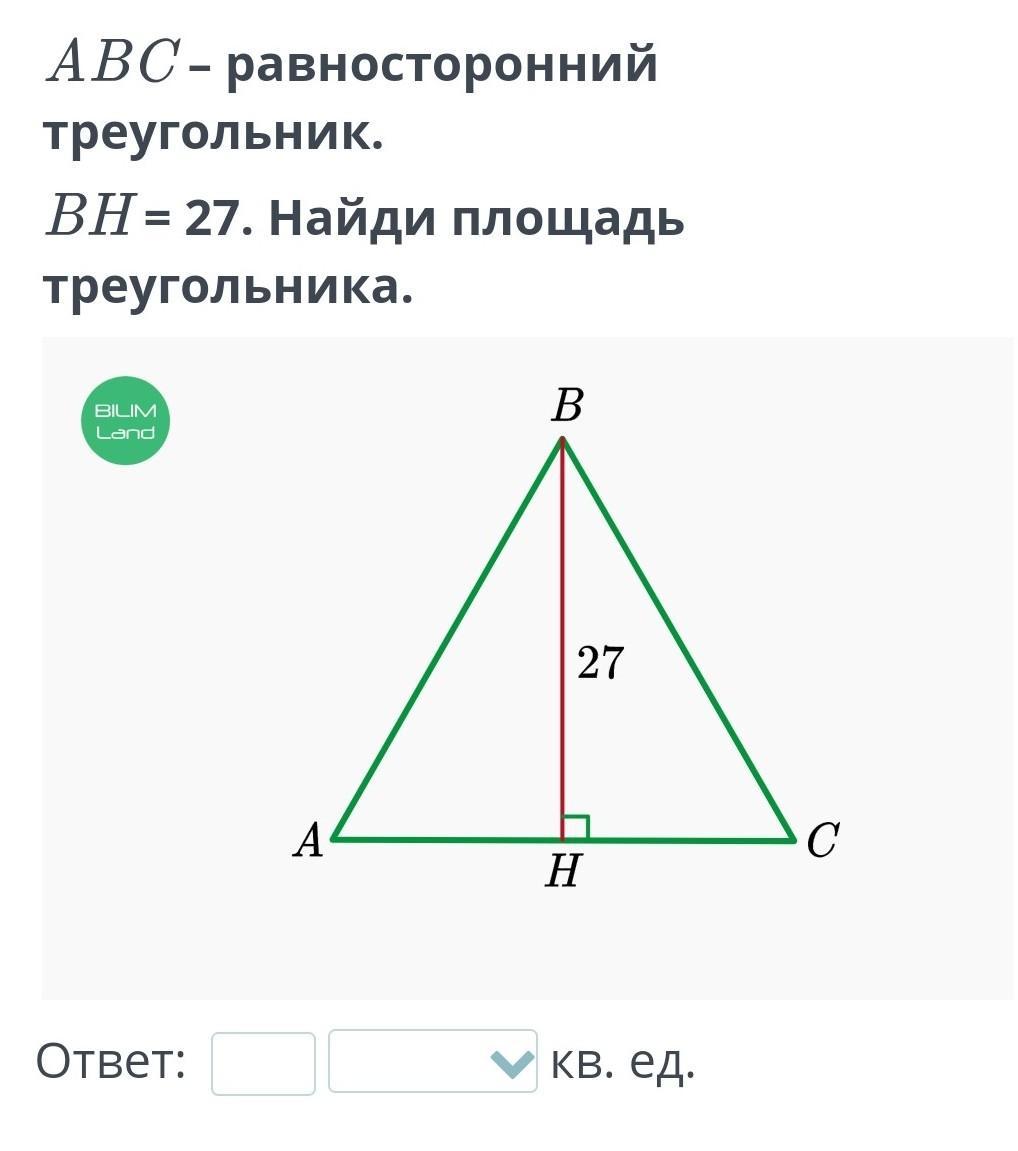
дам 100 баллов ABC – равносторонний треугольник. BH = 27. Найди площадь треугольника. ​

Answer 1

Равносторонний треугольник - тот треугольник, у которого все стороны равны.

$S=\frac{1}{2} *AC*BH$

Где АС-Основание треугольника, а BH - Высота.

$a=\frac{2h}{\sqrt{3} }$

При h=27, 2h=54

Сторона - 54/√3

Площадь- 1/2 * 54/√3 * 27/1 = 1458/2√3 = 1458/√2²*3 = 1458 / √12 = 243√3