Предмет: Алгебра,
автор: yasminobeid
ПОМОГИТЕ ПОЖАЛУЙСТА!
Приложения:
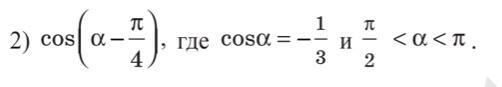
Ответы
Автор ответа:
1
Ответ: (4 - √2)/6
Объяснение: Используем формулу косинуса разности двух углов:
Cos(α - β)=Cosα·Cosβ+Sinα·Sinβ ⇒
Cos(α- π/4)=Cosα·Cos(π/4)+Sinα·Sin(π/4)
Cos(α- π/4)=Cosα·(√2/2)+Sinα·(√2/2)
По условию Сosα= -1/3 ⇒ т.к. Sin²α=1 - Сos²α, то
Sin²α=1 - (-1/3)²=1 -1/9 = 8/9
Sinα =±√(8/9)=±√8/√9=± 2√2/3
Но по условию π/2< α< π , т.е. угол α ∈ 2 четверти, ⇒ Sinα >0 Значит Sinα = 2√2/3
Тогда
Cos(α- π/4)=Cosα· (√2/2) + Sinα· (√2/2) = (-1/3)·(√2/2)+(2√2/3)·(√2/2)
Cos(α- π/4)= - √2/6 + 4/6
Cos(α- π/4)= (4 - √2)/6
Похожие вопросы
Предмет: Английский язык,
автор: mear501
Предмет: Окружающий мир,
автор: 34retrika16
Предмет: Русский язык,
автор: лиза1576
Предмет: История,
автор: stepratkun
Предмет: Информатика,
автор: Dan141444