Question

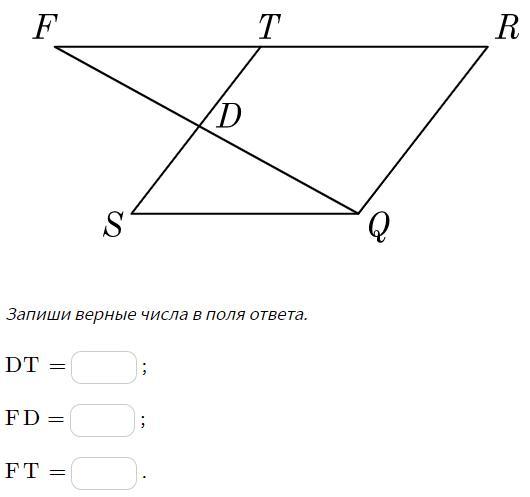
В параллелограмме STRQ точка D делит сторону ST так, что SD:DT = 2:1. Найди стороны треугольника FDT , если SD=18 , DQ=30 , SQ=38 .

Answer 1

Ответ:

Треугольники FDT и FQR подобные, у них угол F общий углы FDT и FQR равны, как соответственные углы. Поэтому треугольники подобные, а у подобных треугольников стороны пропорциональны, то есть FQ/FD=FR/FT=QR/DT=k (k – коэффициент подобия).

SD:DT=2:1

У нас есть SD=18, значит DT=18/2=9.

RQ=ST, потому что у параллелограмма параллельные стороны равны.

RQ=18+9=27.

k=RQ/DT=27/9=3

Коэффициент подобия равен 3.

Обозначим FD как x.

FQ=DQ+FD=30+x

FQ/FD=3

$\frac{30 + x}{x} = 3 \\ 30 + x = 3x \\ 3x - x = 30 \\ 2x = 30 \\ x = 15$

FD=15

SQ=RT, как говорил параллельные стороны равны.

Допустим FT=y

FR=RT+FT

FR=38+y

FR/FT=3

$\frac{38 + y}{y} = 3 \\ 38 + y = 3y \\ 3y - y = 38 \\ 2y = 38 \\ y = 19$

FT=19

Стороны треугольника FDT:

Стороны треугольника FDT:DT=9

Стороны треугольника FDT:DT=9FD=15

Стороны треугольника FDT:DT=9FD=15FT=19