ПОМОГИТЕ
система:


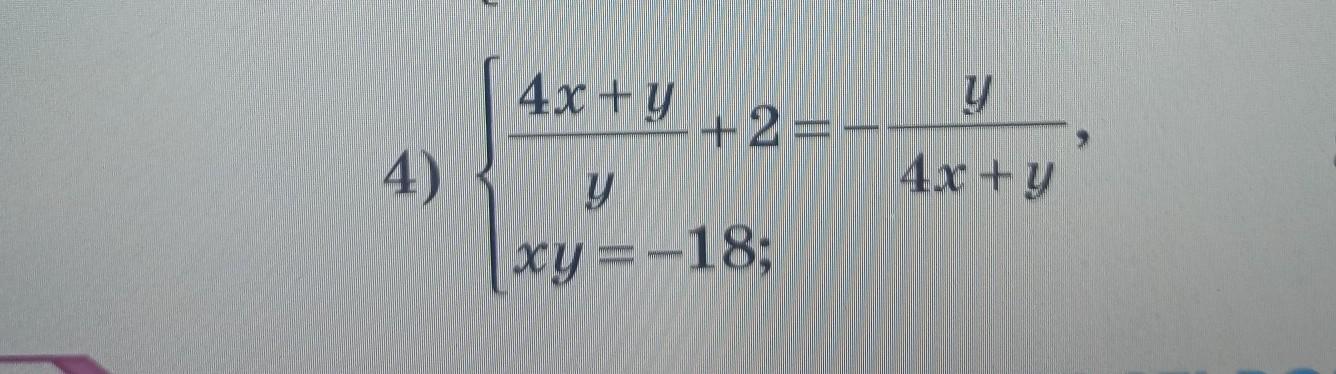
Ответы
Ответ:
В решении.
Объяснение:
Решить систему уравнений:
(4х + у)/у + 2 = - у/(4х + у)
ху = -18
Преобразовать первое уравнение:
Умножить все части уравнения на у(4х + у), чтобы избавиться от дробного выражения:
(4х + у)² + 2у(4х + у) = - у²
16х² + 8ху + у² + 8ху + 2у² + у² = 0
16х² + 16ху + 4у² = 0/4 для упрощения;
4х² + 4ху + у² = 0 - упрощённое первое уравнение;
Выразить х через у во втором уравнении, подставить выражение в первое уравнение и вычислить у:
х = -18/у
4 * (-18/у)² + 4у * (-18/у) + у² = 0
4 * 324/у² - 72 + у² = 0
1296/у² - 72 + у² = 0
Умножить все части уравнения на у², чтобы избавиться от дробного выражения:
1296 - 72у² + у⁴ = 0
у⁴ - 72у² + 1296 = 0
Ввести новую переменную:
у² = t;
t² - 72t + 1296 = 0, квадратное уравнение, ищем корни:
D=b²-4ac = 5184 - 5184 = 0 √D=0
t₁,₂=(-b±√D)/2a
t₁,₂=(72±0)/2
t₁,₂= 36;
Вернуться к первоначальной переменной:
у² = t;
у² = 36
у₁,₂ = ±√36
у₁ = -6;
у₂ = 6;
Вычислить х:
х = -18/у
х₁ = -18/-6
х₁ = 3;
х₂ = -18/6
х₂ = -3;
Решения системы уравнений: (3; -6); (-3; 6).
Проверка путём подстановки вычисленных значений х и у в систему уравнений показала, что данное решение удовлетворяет данной системе уравнений.