Ответы
Ответ:
В решении.
Объяснение:
Графічно розв'яжіть рівняння:
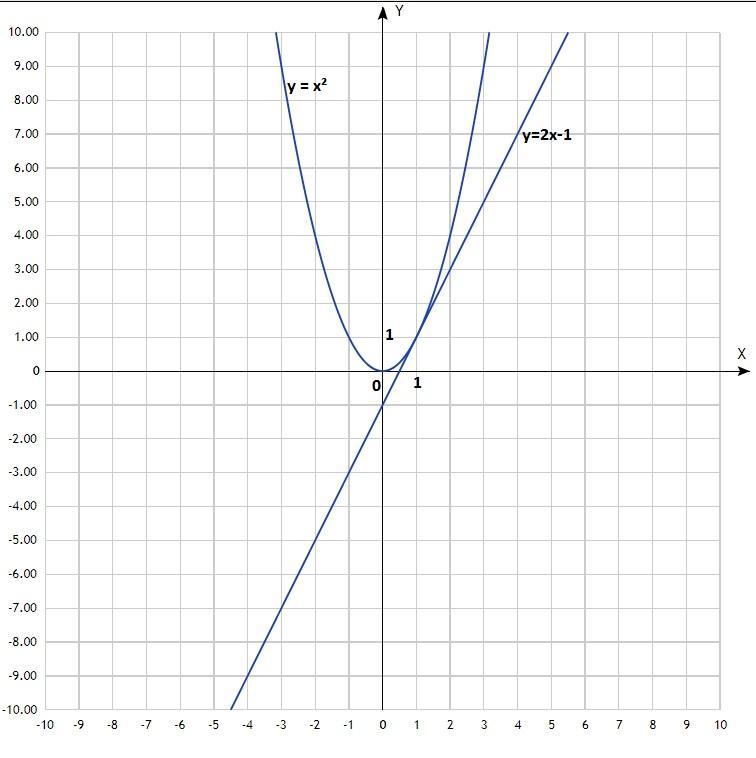
а) х² = 2х – 1;
↓
у = х²; у = 2х - 1;
Построить графики. Первый - классическая парабола с центром в начале координат (0; 0), ветви направлены вверх.
Второй - прямая линия.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = х²; у = 2х - 1;
Таблицы:
х -3 -2 -1 0 1 2 3 x -1 0 1
у 9 4 1 0 1 4 9 у -3 -1 1
По вычисленным точкам построить графики.
Координаты точки пересечения графиков: (1; 1).
Решение уравнения: х = 1.
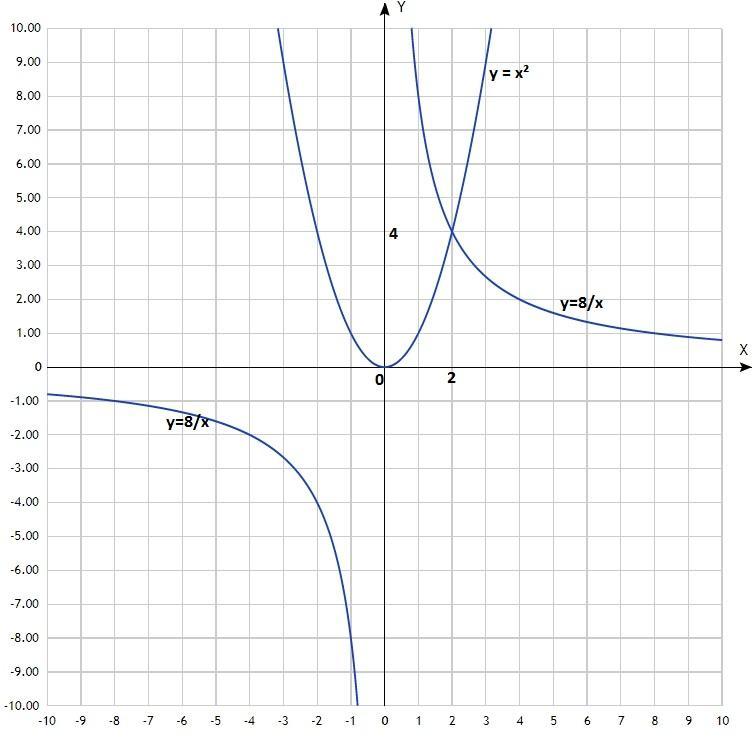
б) х² = 8/х;
↓
у = х²; у = 8/х;
Построить графики. Первый - классическая парабола с центром в начале координат (0; 0), ветви направлены вверх.
Второй - гипербола.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = х²; у = 8/х;
Таблицы:
х -3 -2 -1 0 1 2 3 х -8 -4 -2 -1 0 1 2 4 8
у 9 4 1 0 1 4 9 у -1 -2 -4 -8 - 8 4 2 1
По вычисленным точкам построить графики.
Координаты точки пересечения графиков: (2; 4).
Решение уравнения: х = 2.
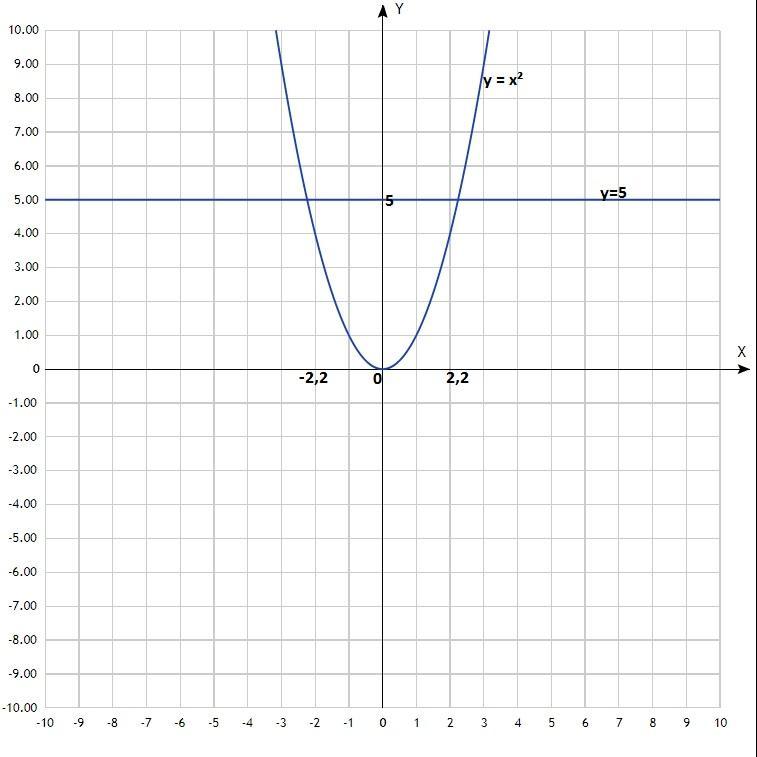
в) х² = 5;
↓
у = х²; у = 5;
Построить графики. Первый - классическая парабола с центром в начале координат (0; 0), ветви направлены вверх.
Второй - прямая линия, параллельная оси Ох и проходящая через точку у = 5.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = х²;
Таблица:
х -3 -2 -1 0 1 2 3
у 9 4 1 0 1 4 9
По вычисленным точкам построить графики.
Координаты точек пересечения графиков: (-2,2; 5); (2,2; 5).
Решение уравнения: х = -2,2; х = 2,2.