Question

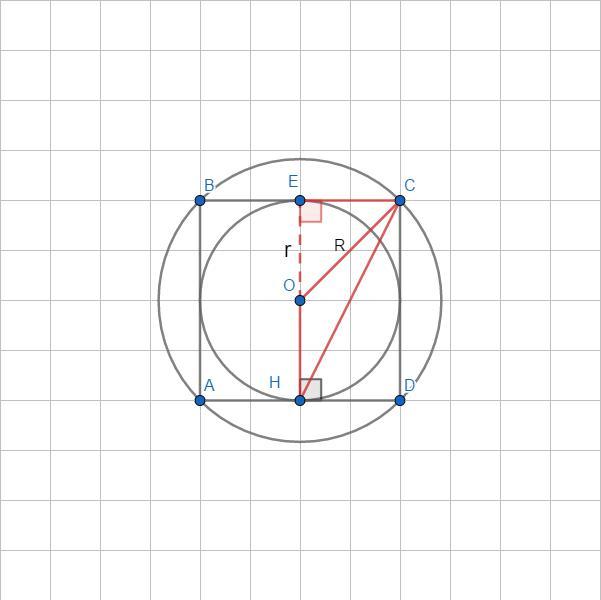
Около квадрата ABCD описана окружность с центром О. Окружность, вписанная в этот квадрат, касается стороны AD в точке Н.
Найти площадь квадрата, если площадь треугольника OCH равна 24.
ПОМОГИТЕ ПОЖАЛУЙСТА, СРОЧНО

Answer 1

Ответ:

• $\boldsymbol{S_{ABCD}=192}$

Объяснение:

• Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.

Проведем радиус ОЕ в точку касания прямой ВС с окружностью ω(О; r), тогда ОЕ⊥ВС и, следовательно, CE⊥EH (радиусы ОЕ и ОН лежат на одной прямой).

Т.к. окружность ω(О; r) касается стороны AD в точке H, то OH⊥AD, ибо OH - радиус, проведенный в точку касания.

• Радиус вписанной окружности равен половине стороны квадрата.
• Окружность, вписанная в квадрат, касается середин сторон этого квадрата.

Пусть AB=BC=CD=AD=x - сторона квадрата, тогда $\displaystyle OE=\boldsymbol {OH=\frac{x}{2} }$ .

Т.к. окружность ω(О; r) вписанная, то $\displaystyle BE= \boldsymbol{EC=\frac{x}{2} }$.

• Площадь треугольника находится по формуле: $\displaystyle \boldsymbol{S=\frac{1}{2} ah}$, где a - сторона треугольника, h - высота, проведенная к этой стороне.
• Площадь квадрата находится по формуле: $\boldsymbol{S=a^2}$, где a - сторона квадрата.

Т.к. CE⊥EH, то CE - высота треугольника ΔOCH, тогда площадь треугольника ΔOCH: $\displaystyle \boldsymbol{S_{\triangle OCH}}=\frac{1}{2}\cdot OH\cdot EC =\frac{1}{2} \cdot \frac{x}{2} \cdot \frac{x}{2} =\boldsymbol{\frac{x^2}{8} =24}$, откуда $\boldsymbol {x^2=192}$.

Площадь квадрата ABCD: $\displaystyle \boldsymbol{S_{ABCD}}=AB^2=x^2= \boldsymbol{192}$.