Предмет: Математика,
автор: 4ynoka6puk
Помогите! Нужна помощь
Приложения:
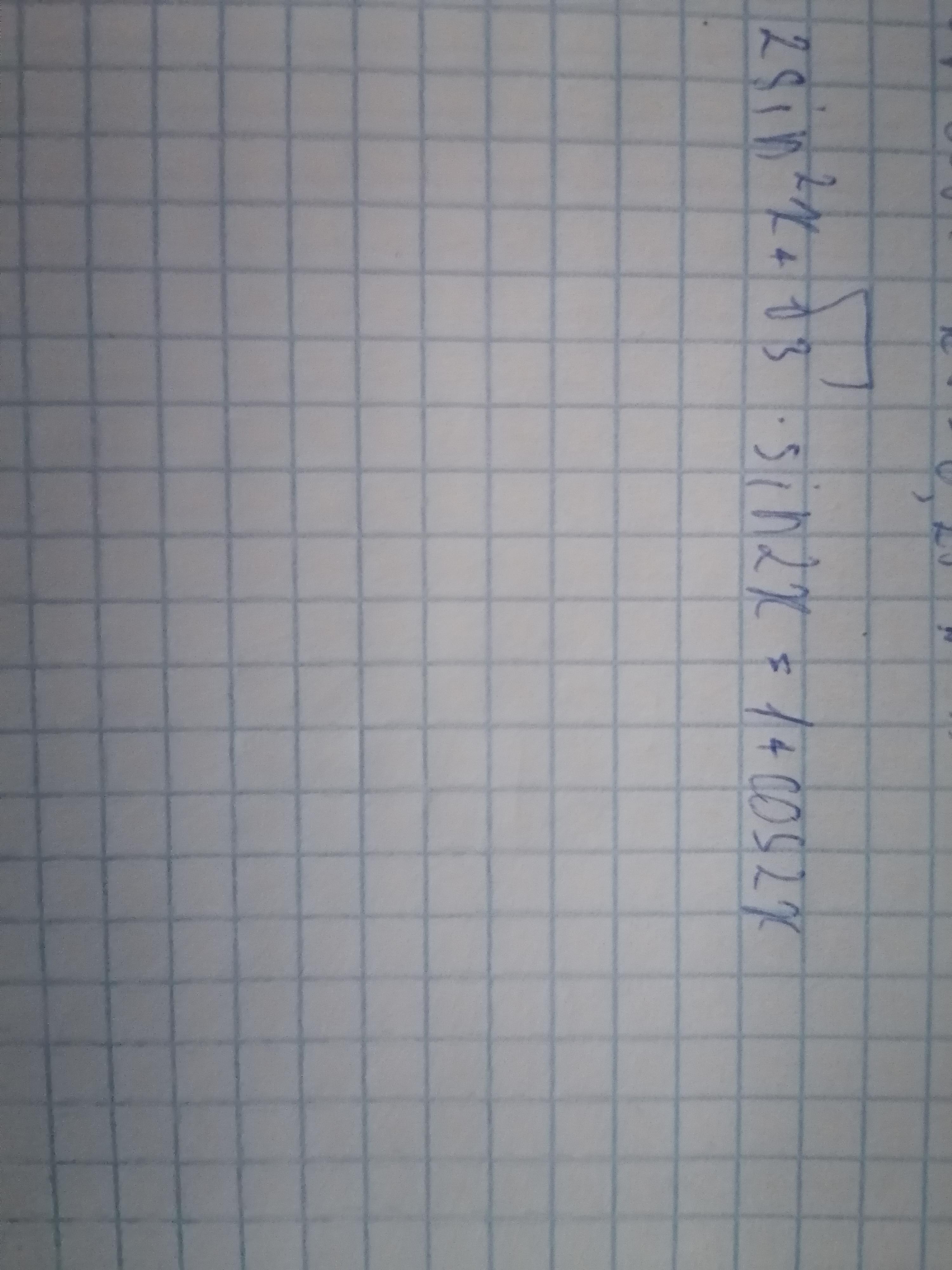
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Английский язык,
автор: bruy1955
Предмет: Окружающий мир,
автор: алекса182
Предмет: Українська література,
автор: dasha200221
Предмет: Биология,
автор: Мишаня0