Question

Реши задачу
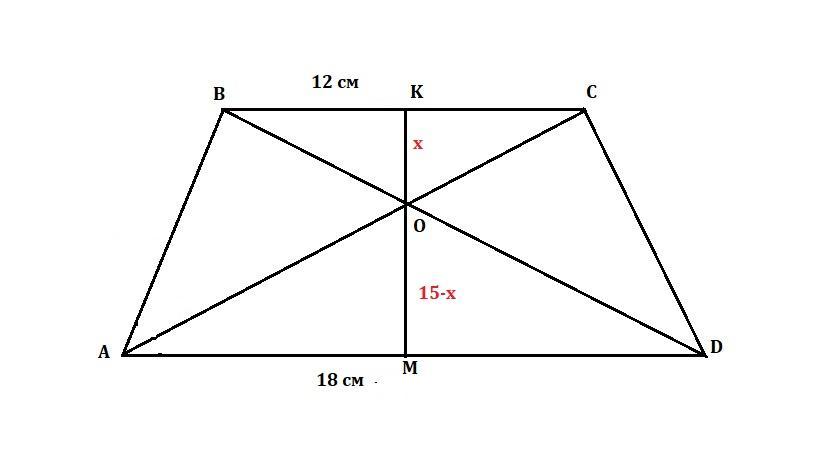
Основания трапеции равны 12 см и 18 см, а высота - 15 см. Найди расстояния от Точки пересечения диагоналей трапеции к её основаниям. Длины укажите в порядке возрастания.
Помогите пожалуйста ​

Answer 1

Ответ:

6 см, 9 см

Объяснение:

Так как основания трапеции параллельны, а диагонали трапеции являются секущими, то ∠BCA=∠CAD, ∠CBD = ∠BAD - как внутренние накрест лежащие углы при параллельных прямых AD и BC и секущих BD и AC.

Следовательно △BOC подобен △ DOA по двум углам (первый признак подобия треугольников).

Коэффициент подобия этих треугольников равен отношению длин сходственных сторон:

$k=\dfrac{BC}{AD} =\dfrac{12}{18} =\dfrac{2}{3}$

Отношение длин соответствующих элементов подобных треугольников равно коэффициенту подобия.

Пусть КО = х см, тогда ОМ = (15-х) см.

Тогда:

$\dfrac{KO}{OM} =k\\\\\dfrac{x}{15-x} =\dfrac{2}{3} \\\\3x=30-2x\\5x=30\\x=6$

КО = 6 cм, ОМ = 15-6 = 9 см