помогите решить задачу
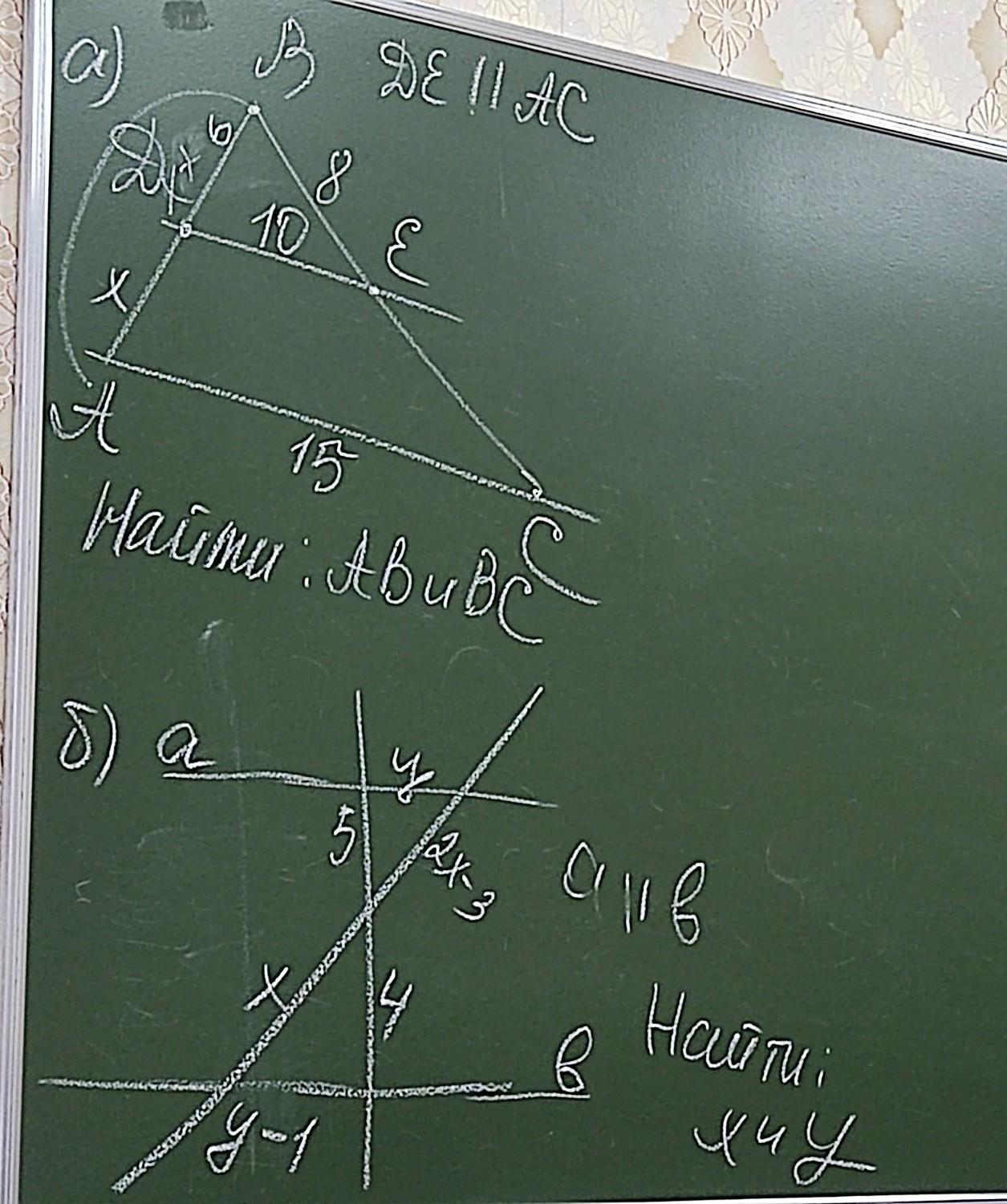
Ответы
а) т.к. треугольники DВЕ и АВС подобны по 1 признаку, у них угол В- общий, углы ВDЕ и ВАС равны как соответственные при параллельных DЕ и АС и секущей АВ, составим пропорцию
DЕ/АС=ВЕ/ВС⇒ВС=АС*ВЕ/DЕ=15*8/10=12
DЕ/АС=ВD/АВ⇒АВ=АС*ВD/DЕ=15*6/10=9
Проверка.
получили отношение сторон ВD/АВ=DЕ/АС=ВЕ/ВС=6/9=10/15=8/12
все отношения после сокращения дают один результат 3/2- решено верно.
Ответ АВ=9; ВС=12
б) треугольник со сторонами у; 5 и 2х-3 подобен треугольнику со сторонами у-1; 4 и х, по первому признаку подобия, т.к. при пересечении двух прямых, образуются у этих треугольников вертикальные углы, они равны, а два других внутренние накрест лежащие тоже равны, при параллельных а и b и секущей , содержащей отрезки 5 и 4, составим пропорции
у/(у-1)=5/4=(2х-3)/х;
у/(у-1)=5/4⇒по основному свойству пропорции 4у=5у-5; у=5,
5/4=(2х-3)/х⇒по основному свойству пропорции 8х-12=5х; 3х=14, х=4
Ответ х=4; у=5