Предмет: Геометрия,
автор: tsetsulinayana
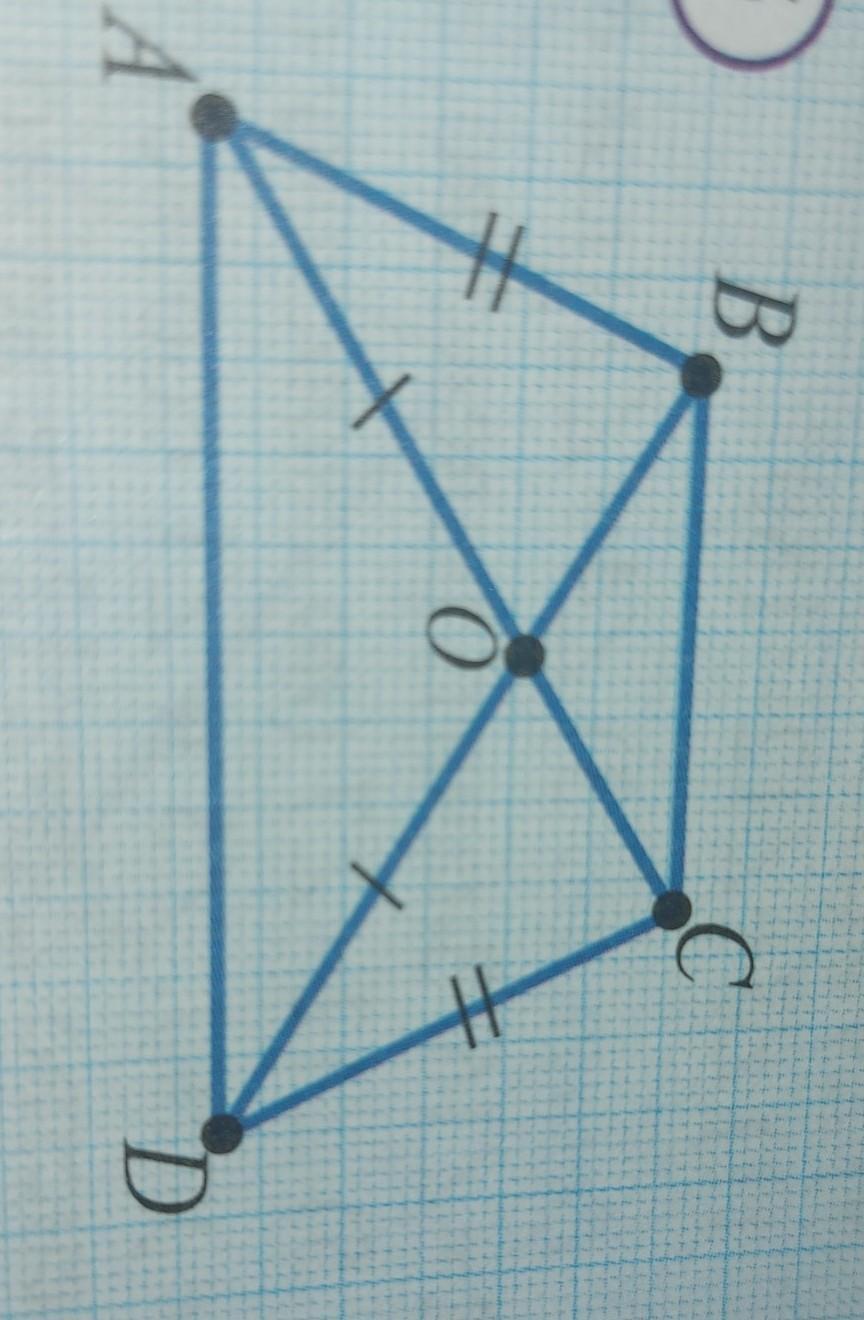
Известно, что ВС||AD, АО=ОD, докажите, что АС=ВD
СРОЧНО, ДАМ МНОГО БАЛЛОВ!! только все четко и ясно, заранее спасибо!!!!!
Приложения:
Ответы
Автор ответа:
1
т.к. АD║ВС, и АВ=СD⇒ АВСD- равнобедренная трапеция по отпределению. Но тогда ∠ВDА=∠ DAС, как углы при основании АD,
Рассмотрим треугольники АВD DCA, у них АD-общая, АВ=СD- по условию, и по первому признаку подобия эти треугольники равны.
а в равных треугольниках против равных углов лежат равные стороны АС и BD, доказано. условие АО=ОD считаю лишним.
2 способ. можно совсем коротко по свойству диагоналей равнобедренной трапеции АС=ВD
marshal500:
в равнобедренной трапеции диагонали равны. своей первой фразой Вы уже доказали АС = BD... все остальное - вода...
Автор ответа:
1
Ответ:
по первому признаку равенства треугольников угол AOB=COD значит BO=OC угол BOC=AOD потому что они вертикальные
Объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: Мультимир
Предмет: Русский язык,
автор: Мasha1
Предмет: Литература,
автор: 1736dh
Предмет: Литература,
автор: natasha300682