Предмет: Алгебра,
автор: sashonoxin2003
Помогите пожалуйста решить 2 вар
Приложения:
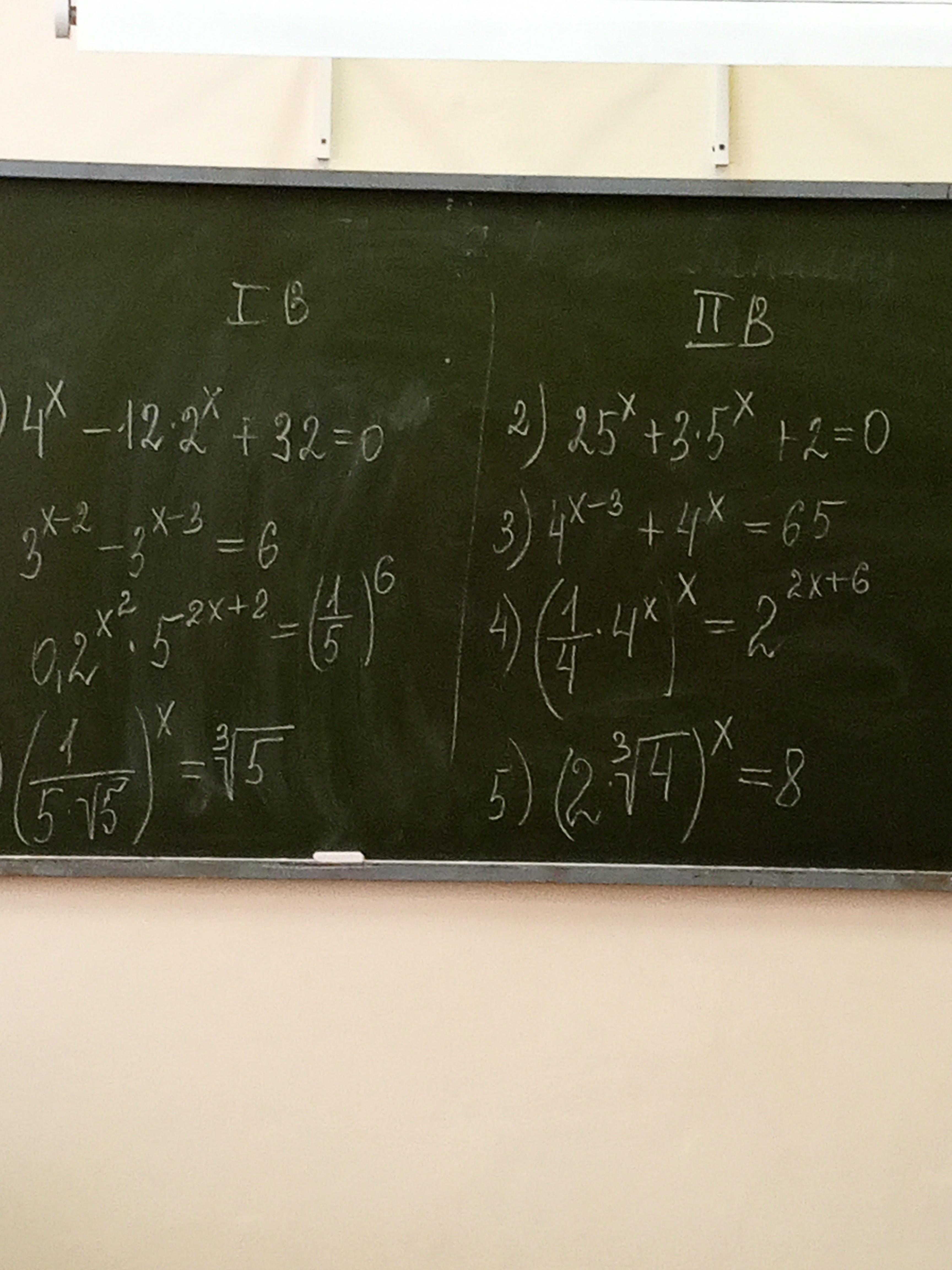
Ответы
Автор ответа:
1
Ответ:
Так как показательная функция может принимать только положительные значения , то отрицательные значения -2 и -1 не подходят ,
.
Ответ: нет решений .
Похожие вопросы
Предмет: Русский язык,
автор: Tarsen2005
Предмет: Русский язык,
автор: cvyu
Предмет: Технология,
автор: polina162005
Предмет: Русский язык,
автор: 55544475
Предмет: Английский язык,
автор: Qwerty1929