Question

Дан треугольник АВС. Через центр О окружности, проведенной к ней извне, был проведен перпендикуляр I к плоскости АВС. Докажите, что каждая точка l находятся на одинаковом расстоянии от вершин A, B, C. ​

Answer 1

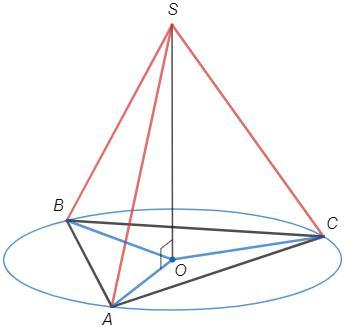
О - центр описанной окружности, OA=OB=OC (радиусы)

S - произвольная точка на прямой L.

Прямая L перпендикулярна плоскости ABC и любой прямой в этой плоскости.

SO⊥(ABC) => SO⊥OA, SO⊥OB, SO⊥OC

△SOA=△SOB=△SOC (по двум катетам, SO - общий) => SA=SB=SC