Предмет: Алгебра,
автор: wrskkmkgs5
Знайдіть область визначення функції
Пожалуйста, очень надо(((
Приложения:
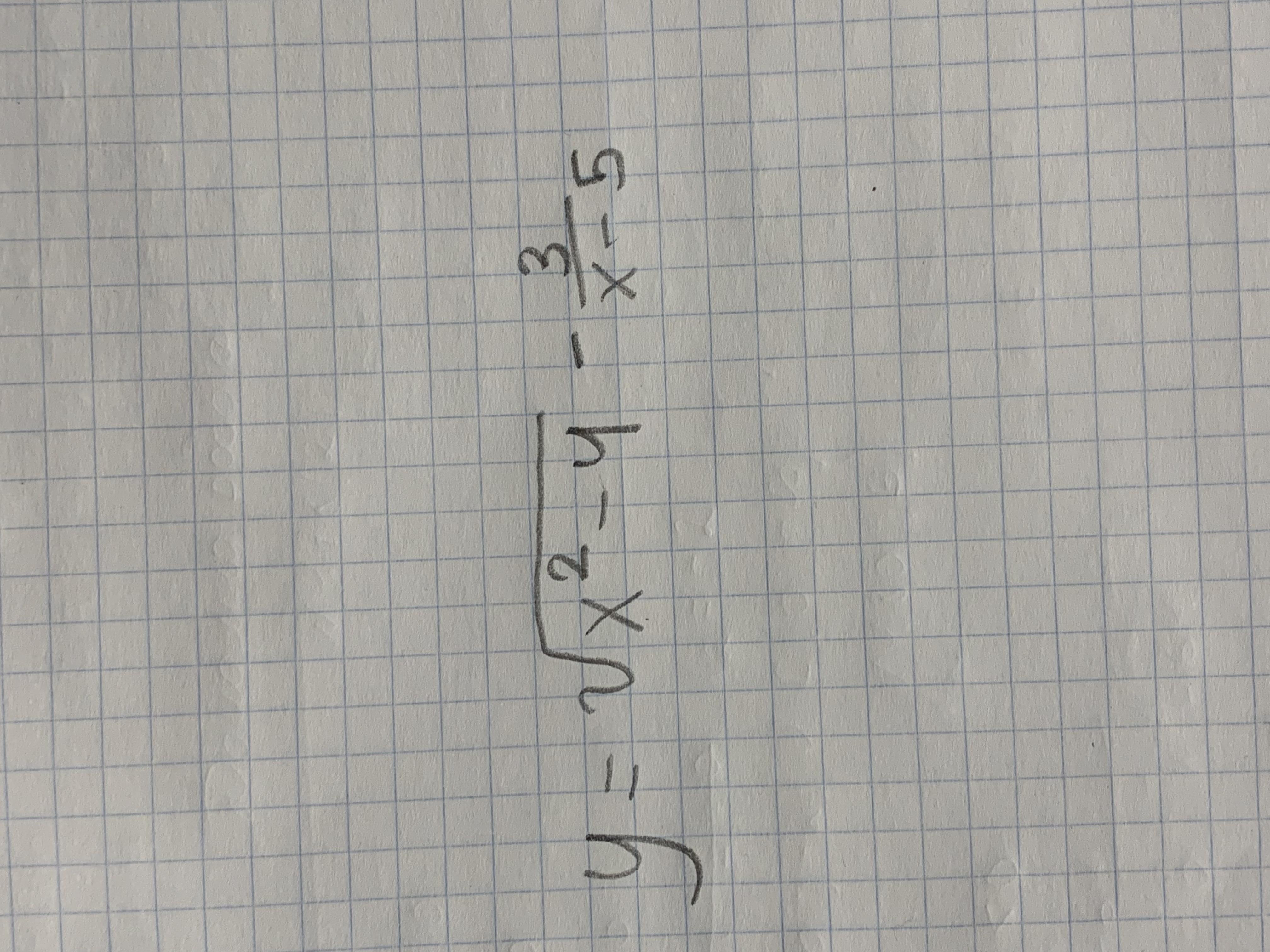
Ответы
Автор ответа:
1
Ответ:
Область определения функции
D(y) = (-∞; -2] ∪ [2; 5) ∪ (5; +∞)
Объяснение:
Требуется найти область определения функции.
- Область определения функции — это множество всех значений аргумента (переменной x)
Используем следующие правила:
- Подкоренное выражение неотрицательно.
- На ноль делить нельзя!
Получим систему:
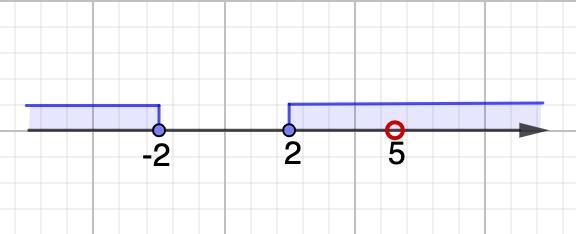
Отметим решение на числовой оси.(см.рис)
Получим ответ:
D(y) = (-∞; -2] ∪ [2; 5) ∪ (5; +∞)
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: Аноним
Предмет: Русский язык,
автор: romanenkova84
Предмет: Русский язык,
автор: дракон88
Предмет: Математика,
автор: anastasiyatryas
Предмет: История,
автор: Аноним