Question

ПОМОГИТЕ СРОЧНО!
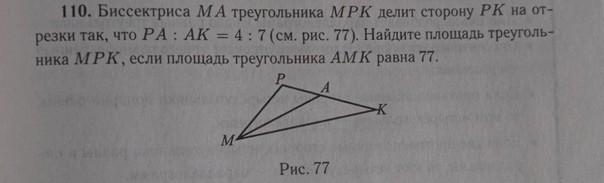
110. Биссектриса МА треугольника МРК делит сторону РК на отрезки так, что РА : AK = 4 : 7 (см. рис. 77). Найдите площадь треугольника МРК, если площадь треугольника АМК равна 77.​​

Answer 1

У ΔMPA и ΔAMK высоты равны (пусть h - их общая высота), тогда $\displaystyle \frac{S_{MPA}}{S_{AMK}}=\frac{\frac{1}{2} \cdot h \cdot PA}{\frac{1}{2} \cdot h \cdot AK} =\frac{PA}{AK} =\frac{4}{7}$.

Откуда $\displaystyle S_{MPA}=\frac{S_{AMK} \cdot 4}{7}=\frac{77 \cdot 4}{7} =44$.

Значит, $\displaystyle S_{MPK}=S_{MPA}+S_{AMK}=44+77=121$.

Ответ: 121.