Предмет: Алгебра,
автор: Аноним
.................Срочно
Приложения:
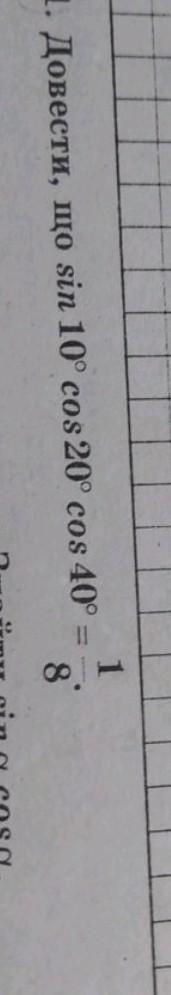
Ответы
Автор ответа:
1
Ответ:
Все внутри использованные формулы:
Автор ответа:
1
Ответ:
Объяснение:
!!!!!!!!!!!!!!!!!!!!!!!
Приложения:

Похожие вопросы
Предмет: Қазақ тiлi,
автор: lauratyuteeva
Предмет: Русский язык,
автор: evelinaaanisim
Предмет: Русский язык,
автор: Звёздочка20051
Предмет: Математика,
автор: sungat11
Предмет: Литература,
автор: cizkovsemen