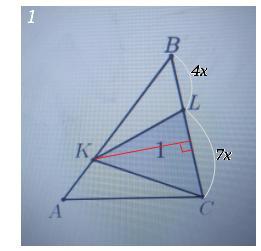
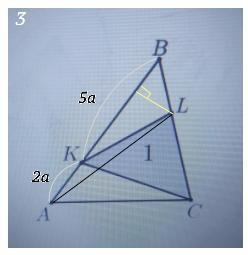
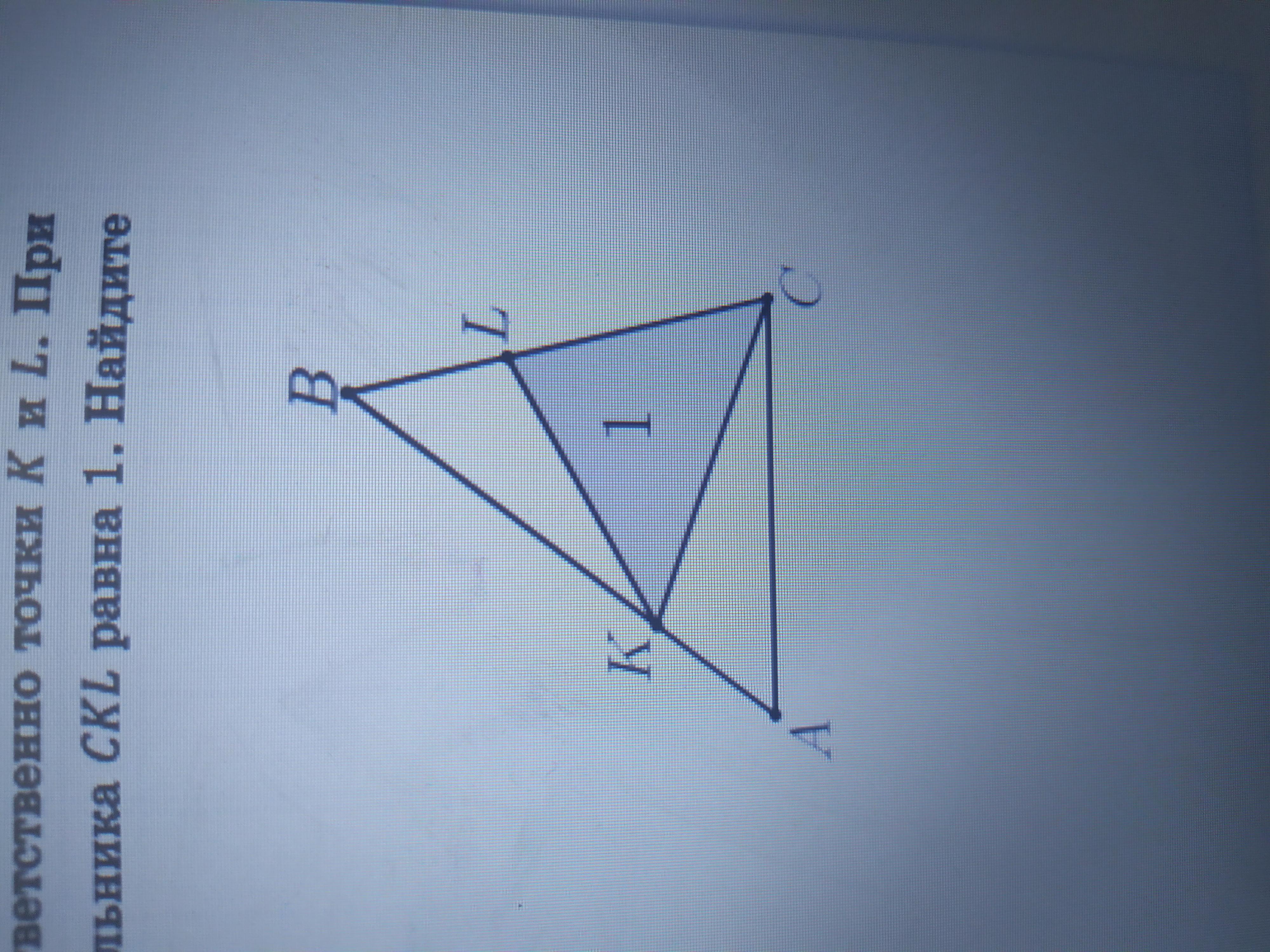
5. На сторонах АВ и ВС треугольника АВС взяты соответственно точки К и L. При этом AК : KB = 2 : 5, BL : LC = 4 : 7. Площадь треугольника CKL равна 1. Найдите площади треугольников ABC и AKL.
ПОМОГИТЕ СРОЧНО.
Ответы
Ответ: Ѕ(АВС)=(11/7):5•7=11/5=2 ¹/₅; Ѕ(AKL ) =8/35 (ед. длины)
Объяснение ( подробно):
Одна из формул площади треугольника Ѕ=h•a/2, где h- высота, а - основание. =>
Площади треугольников, имеющих одинаковую высоту, относятся как основания, к которым проведена эта высота.
1) ∆ ВКС и ∆ ВКL имеют общую вершину К и общую высоту к прямой ВС, содержащей их основания CL и BL.
Тогда из отношения длин их оснований
Ѕ(CKL):Ѕ(ВКL)=7:4, откуда Ѕ(ВКL)=1:7•4=4/7
Ѕ(ВКС)= Ѕ(CKL)+Ѕ(ВКL)=7/7+4/7=11/7=1 ⁴/₇.
2) ∆ ВКС и ∆ АВС имеют общую вершину С и общую высоту к прямой, содержащей их основания КВ и АВ. Отношение их оснований КВ:АВ=5:(2+5)=5:7 =>
Ѕ(ВКС):Ѕ(АВС)=5/7
Ѕ(АВС)=(11/7):5•7=11/5=2 ¹/₅ ( ед. длины)
3) ∆ AKL и ∆ BKL имеют общую высоту вершину L и общую высоту. =>
Ѕ(AKL ):Ѕ(BKL)=2:5
Ѕ(AKL )=Ѕ(BKL):5•2
Ѕ(AKL )=(4/7):5•2 =8/35 (ед. длины)