Question

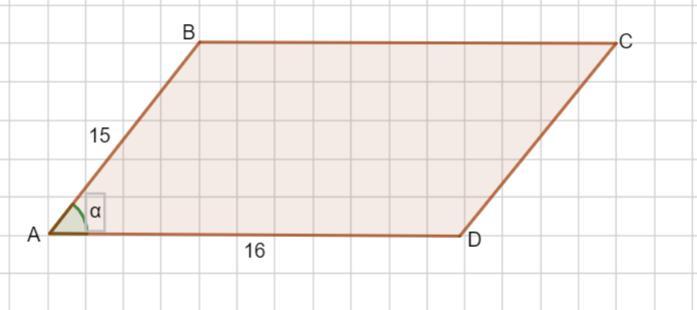
Одна из сторон параллелограмма равна 16, другая равна 15, а косинус одного из углов равен корень из 7 деленный на 4 (√‎7/4). Найдите площадь параллелограмма

Answer 1

Ответ:

180 кв. ед.

Пошаговое объяснение:

Пусть  ABCD - параллелограмм.  АВ= 15, AD=16, ∠ А=α ,

$\cos\alpha =\dfrac{\sqrt{7} }{4}$

(косинус острого угла есть число положительное)

Площадь параллелограмма определяется по формуле

$S=a\cdot b\cdot sin \alpha ,$   где a,b- стороны параллелограмма, α - угол между ними.

Найдем синус угла, для этого воспользуемся основным тригонометрическим тождеством.

$sin^{2} \alpha +cos^{2} \alpha =1;\\sin^{2} \alpha=1-cos^{2} \alpha ;\\sin\alpha =\pm\sqrt{1-cos^{2} \alpha } ;$

Так как угол острый, то синус положительный. Тогда

$sin\alpha =\sqrt{1-\left(\dfrac{\sqrt{7} }{4}\right)^{2} } =\sqrt{1-\dfrac{7}{16} } =\sqrt{\dfrac{16}{16} -\dfrac{7}{16} } =\sqrt{\dfrac{9}{16}} =\dfrac{3}{4}$

Тогда найдем площадь параллелограмма

$S=AB\cdot AD\cdot sin A;\\\\S=15\cdot16\cdot \dfrac{3}{4} =\dfrac{15\cdot16\cdot3}{4} =\dfrac{15\cdot4\cdot4 \cdot3}{4} =\dfrac{15\cdot4\cdot3}{1} =180$

Значит, площадь параллелограмма равна 180 кв. ед.