Question

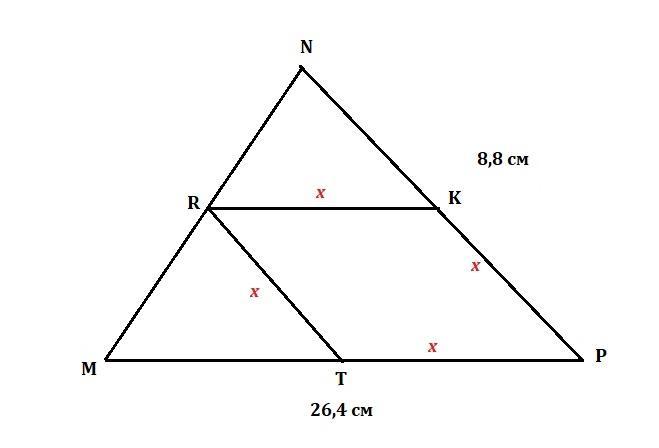
Ромб RTPK вписан в треугольник MNP так, что точка R лежит на стороне МN, а угол P - общий.
Чему равна сторона ромба RTPK, если стороны треугольника МP и NP равны 26,4 см и 8,8 см, соответственно.

Answer 1

Ответ:

Сторона ромба равна 6,6 см.

Объяснение:

Ромб - это параллелограмм, у которого все стороны  равны, а противоположные стороны параллельны:  RK ║ MP.

1) Рассмотрим ΔRNK и ΔMNP.

∠NKR = ∠NPM - как соответственные углы при параллельных прямых RK и MP и секущей NP.

∠N - общий.

Следовательно ΔRNK подобен ΔMNP по двум углам (первый признак подобия).

В подобных треугольниках соответственные стороны пропорциональны:

$\dfrac{RK}{MP} =\dfrac{NK}{NP}$

Пусть сторона ромба равна х см. Тогда RK = x см, NК = (8,8-х) см.

$\dfrac{x}{26,4} =\dfrac{8,8-x}{8,8}$

Умножим обе части равенства на 26,4:

х=3(8,8-х)

х=26,4-3х

4х=26,4

х=6,6

Сторона ромба равна 6,6 см.