Question

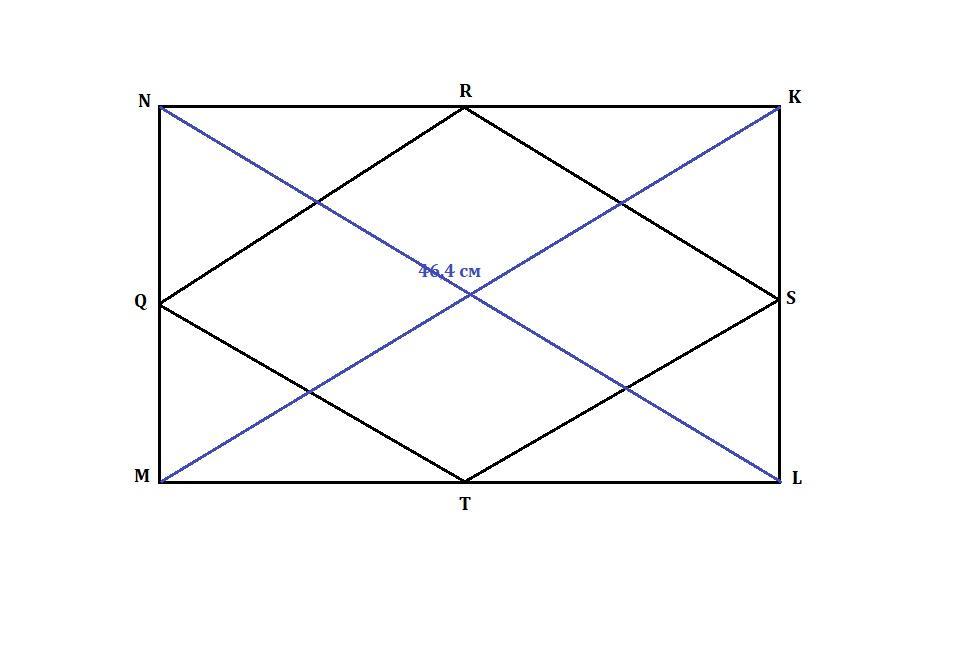
В прямоугольнике MNKL точки Q, R, S и T являются серединами его сторон. Чему равен периметр четырёхугольника QRST, если диагональ прямоугольника MNKL равна 46,4 см.​

Answer 1

Ответ:

92,8 см

Объяснение:

Так как MNKL - прямоугольник, то его противоположные стороны попарно равны: MN = KL, NK = ML.

Диагонали прямоугольника равны: МК=NL.

Q, R, S и T - середины сторон прямоугольника ⇒

MQ=QN=KS=SL, NR=RK=MT=TL.

• Средняя линия треугольника — отрезок, который соединяет середины двух сторон

QR - средняя линия ΔMNK, RS - средняя линия ΔNKL, TS-средняя линия ΔMKL, QT- средняя линия ΔNML.

• Средняя линия параллельна третьей стороне, а ее длина равна половине длины этой стороны

QR = $\frac{1}{2}$ * МК =  $\frac{1}{2}$ * 46,4 = 23,2 см

TS = $\frac{1}{2}$ * МК =  $\frac{1}{2}$ * 46,4 = 23,2 см

RS = $\frac{1}{2}$ * NL =  $\frac{1}{2}$ * 46,4 = 23,2 см

QT = $\frac{1}{2}$ * NL =  $\frac{1}{2}$ * 46,4 = 23,2 см

Периметр четырёхугольника QRST:

Р=QR+TS+RS+QT=4*23,2=92,8 см