Предмет: Геометрия,
автор: kivikivi95
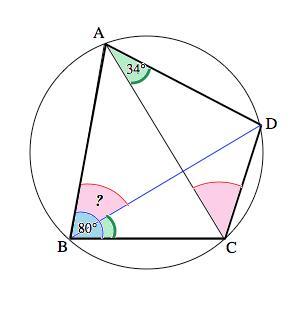
Четырехугольник ABCD вписан в окружность. Угол ABC=80, угол CAD=34. Найдите угол ABD
Ответы
Автор ответа:
2
Решение на фото: тут используется свойство угла вписанного в окружность
Приложения:

Автор ответа:
4
Ответ:
Объяснение: ∠АВD=46°
Объяснение:
Четырехугольник ABCD вписан в окружность.
Дается два варианта решения.
а) Сумма противоположных углов вписанного в окружность четырехугольника – 180°. =>
∠ADC=180°-80°=100°. Тогда из суммы углов треугольника в ∆ АDС
∠ ACD=180°-(<ADC+DAC)=46°
Вписанные углы, которые опираются на равные дуги, равны.
∠АВD и ∠АCD опираются на одну дугу DC =>
——————
б) Углы CВD и САD опираются на одну дугу DC.
Вписанные углы, которые опираются на равные дуги, равны. => ∠CВD=∠CAD=34°
∠АВD=∠АВС- ∠СВD=80°-34°=46°
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: nek8
Предмет: Русский язык,
автор: Masha15151525
Предмет: Русский язык,
автор: ЮлёнАли
Предмет: Другие предметы,
автор: hasenovakamilla
Предмет: Русский язык,
автор: drofa65