Question

две окружности с радиусом 6 и 8 пересекаются в двух точках. расстояние между их центрами равна 12 см. Прямая проходящая через точку пересечения P пересекает эти окружности во второй раз в точках Q и R. Если PQ=PR, то найдите PQ2(квадрат)

Answer 1

Ответ:

130

Пошаговое объяснение:

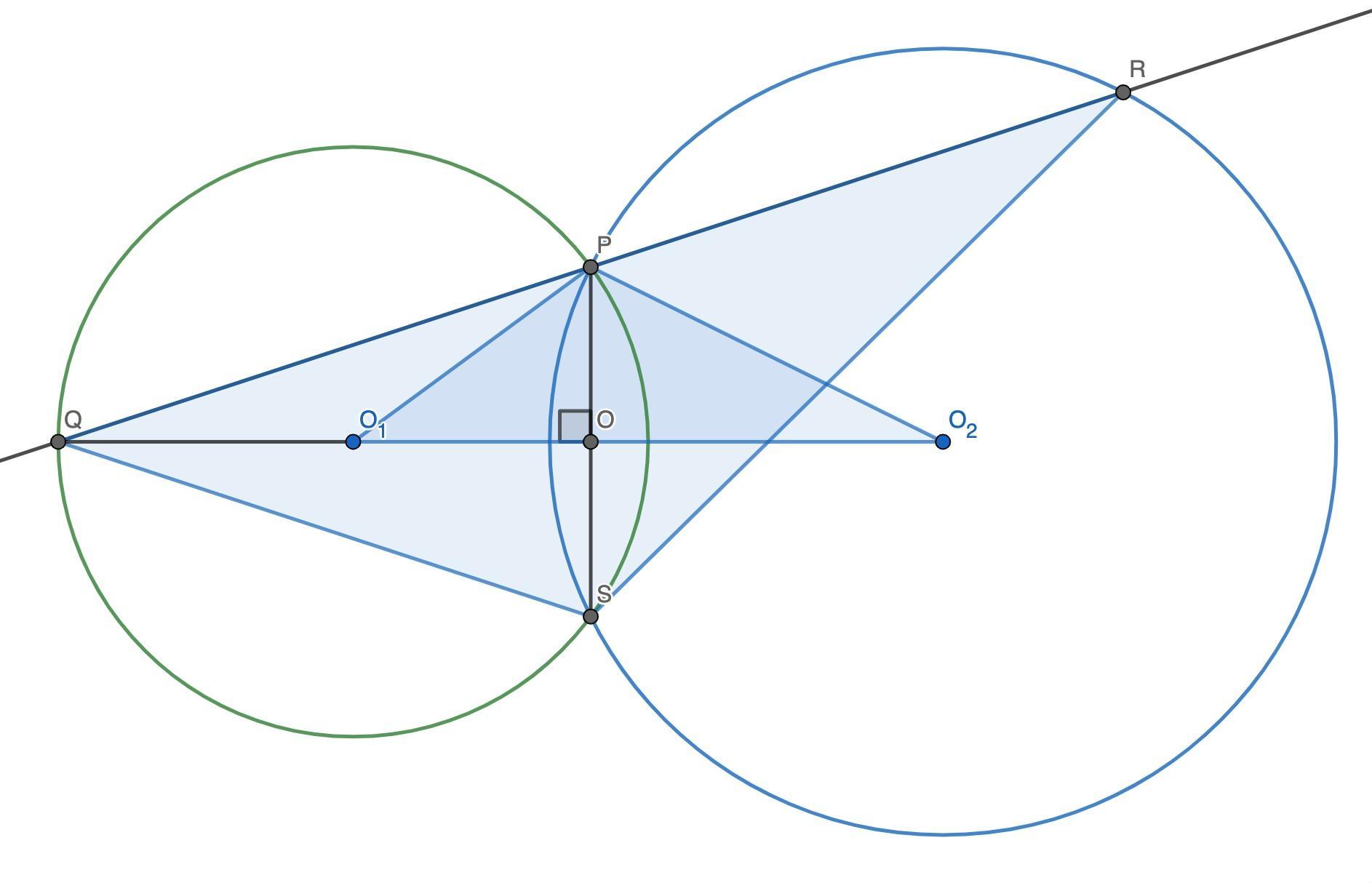
Для определённости назовём центр меньшей окружности O₁, центр большей — O₂, точку пересечения прямой QR и меньшей окружности Q, точку пересечения QR и большей окружности R (не теряя общности, так как отрезки равны), вторую точку пересечения окружностей — S, точку пересечения линии центров и PS — O.

Треугольники O₁PS и O₂PS равнобедренные (боковые стороны — радиусы соответствующих окружностей), значит, O₁O₂ — биссектриса углов ∠PO₁S и ∠PO₂S. Тогда ∠PO₁O = ∠PO₁S / 2, ∠PO₂O = ∠PO₂S / 2.

∠PQS — вписанный для центрального угла ∠PO₁S, ∠PRS — вписанный для центрального угла ∠PO₂S. Тогда ∠PQS = ∠PO₁S / 2 = ∠PO₁O, ∠PRS = ∠PO₂S / 2 = ∠PO₂O.

∠PQS = ∠PO₁O, ∠PRS = ∠PO₂O, следовательно, треугольники O₁PO₂ и QSR подобны по двум углам. Поскольку O₁P : PO₂ : O₁O₂ = 6 : 8 : 12, то и QS : SR : QR = 6 : 8 : 12, отсюда QS : QR = 6 : 12 = 1 : 2. Но QP = PR, значит, QS : QP = QS : (0,5QR) = 1 : (0,5·2) = 1 : 1, значит, QS = QP.

Таким образом, точки Q, O₁, O₂ равноудалены от концов отрезка PS, значит, они лежат на серединном перпендикуляре к PS. В таком случае ∠O = 90°.

По теореме косинусов для треугольника O₁PO₂:

$O_2P^2=O_1P^2+O_1O_2^2-2\cdot O_1P\cdot O_1O_2\cdot\cos{\angle{PO_1O_2}}\\8^2=6^2+12^2-2\cdot 6\cdot 12\cdot\cos{\angle{PO_1O_2}}\\\cos{\angle{PO_1O_2}}=\dfrac{29}{36}\Rightarrow \sin{\angle{PO_1O_2}}=\sqrt{1-\left(\dfrac{29}{36}\right)^2}=\dfrac{\sqrt{455}}{36}$

Поскольку ∠PQS = ∠PO₁O, их синусы также равны. По теореме синусов для треугольника PQS, вписанного в окружность радиусом r = 6:

$PS=2r\cdot\sin{\angle{PQS}}=\dfrac{\sqrt{455}}{3}\Rightarrow PO=\dfrac{PS}{2}=\dfrac{\sqrt{455}}{6}$

Поскольку PQS — равнобедренный, QO — биссектриса угла ∠Q. Тогда $\sin{\angle{PQO}}=\sin{\dfrac{\angle{PQS}}{2}}=\sqrt{\dfrac{1-\cos{\angle{PQS}}}{2}}=\sqrt{\dfrac{1-\dfrac{29}{36}}{2}}=\dfrac{\sqrt{14}}{12}$. При этом $\sin{\angle{PQO}}=\dfrac{PO}{PQ}\Rightarrow PQ=\dfrac{PO}{\sin{\angle{PQO}}}=\dfrac{\sqrt{455}}{6}\cdot\dfrac{12}{\sqrt{14}}=\sqrt{130}$. Тогда PQ² = 130.