Предмет: Алгебра,
автор: larakriss9
определите знак выражения
1)cos255°sin200°tg101°
2)
Полное решение пожалуйста
Приложения:
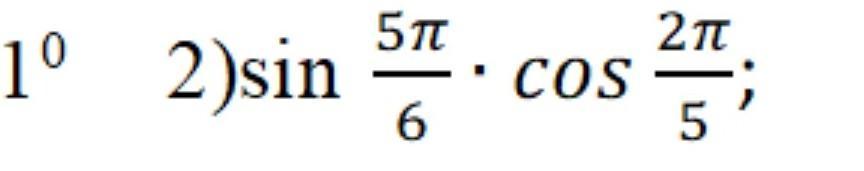
Ответы
Автор ответа:
4
Ответ:
Определим, в каких четвертях лежат углы. В зависимости от этого определим знак каждой функции.
Косинус угла 3 четверти отрицателен , синус угла 3 четверти отрицателен, тангенс угла 2 четверти отрицателен, поэтому их произведение отрицательно .
Определим, в каких четвертях лежат углы. В зависимости от этого определим знак каждой функции.
- угол 2 четверти
Синусы углов 2 четверти положительны , .
- угол 1 четверти
Косинусы углов 1 четверти положительны .
Значит, произведение положительных значений даст положительное число .
larakriss9:
спасибо большое
Похожие вопросы
Предмет: Русский язык,
автор: сармат3
Предмет: Русский язык,
автор: lizik04
Предмет: Қазақ тiлi,
автор: Regina234
Предмет: Русский язык,
автор: guller0110
Предмет: Алгебра,
автор: musya2017