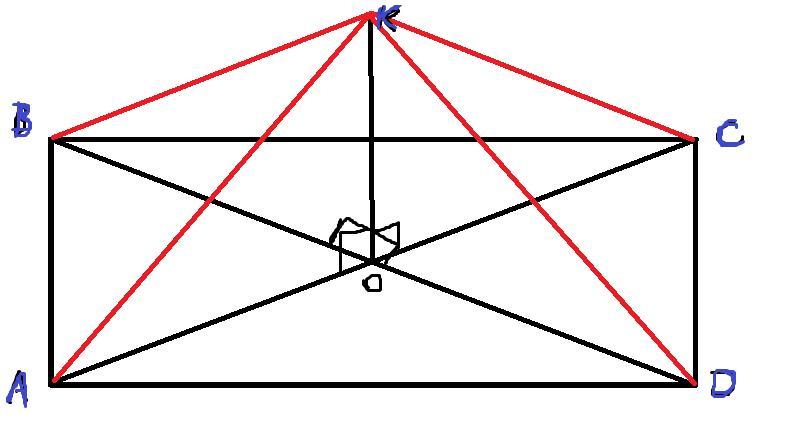
Із точки О- перетину діагоналей прямокутника , до його площини проведено перпендикуляр ОК. Доведіть ,що точка К рівновіддалена від вершин прямокутника.
Ответы
Ответ:
Якщо деяка точка рівновіддалена від вершин многокутника, то основа перпендикуляра, опущеного з даної точки на площину многокутника, збігається з центром кола, описаного навколо многокутника.
Объяснение:
Точка O - центр пересечения диагоналей(+диагонали прямоугольника равны), значит OA=OB=OC=OD
Рассмотрим треугольник AKC:
1)AO=OC
2)OK-общая
3)Угол AOK= Угол COK
Из этого следует что треугольники AOK и COK равны.
Рассмотрим треугольник BKD:
1)BO=OD
2)OK-общая
3)Угол BOK= Угол DOK
Из этого следует что треугольник BOK и DOK равны.
Так же можно рассмотреть остальные две пары треугольников(AOK и BOK, COK и DOK) и сделать вывод что все угольники (AOK,BOK,COK,DOK) равны между собой, а значит гипотенузы у них всех равны, а значит точка K равноудалена от точек A,B,C,D.