Срочно нужна помощь!!
Про многочлен P(x) четвёртой степени известно, что для любого вещественного x выполнено P(x) >= 0, а также P(1) = 0, P(2) = 3, P(3) = 0 . Найдите P(4).
Ответы
Ответ:
P(4) = 27
Объяснение:
Многочлен 4 степени записывается так:
P(x) = ax^4 + bx^3 + cx^2 + dx + e
Нам известны значения:
P(1) = a*1^4 + b*1^3 + c*1^2 + d*1 + e = a + b + c + d + e = 0
P(2) = a*2^4 + b*2^3 + c*2^2 + d*2 + e = 16a + 8b + 4c + 2d + e = 3
P(3) = a*3^4 + b*3^3 + c*3^2 + d*3 + e = 81a + 27b + 9c + 3d + e = 0
Кроме того, нам известно, что этот многочлен при любом x принимает значения P(x) >= 0.
Это значит, что в точках x = 1 и x = 3 он имеет минимумы, равные 0.
Берем производную P'(x):
P'(x) = 4x^3 + 3bx^2 + 2cx + d
Мы знаем, что она равна 0 при x = 1 и при x = 3:
P'(1) = 4a*1^3 + 3b*1^2 + 2c*1 + d = 4a + 3b + 2c + d = 0
P'(3) = 4a*3^3 + 3b*3^2 + 2c*3 + d = 108a + 27b + 6c + d = 0
Получили систему 5 линейных уравнений с 5 неизвестными.
{ a + b + c + d + e = 0 (1)
{ 16a + 8b + 4c + 2d + e = 3 (2)
{ 81a + 27b + 9c + 3d + e = 0 (3)
{ 4a + 3b + 2c + d = 0 (4)
{ 108a + 27b + 6c + d = 0 (5)
Умножаем (1) на -16 и складываем с (2).
Умножаем (1) на -81 и складываем с (3).
Умножаем (1) на -4 и складываем с (4).
Умножаем (1) на -108 и складываем с (5).
{ a + b + c + d + e = 0 (1)
{ 0a - 8b - 12c - 14d - 15e = 3 (2)
{ 0a - 54b - 72c - 78d - 80e = 0 (3)
{ 0a - b - 2c - 3d - 4e = 0 (4)
{ 0a - 81b - 102c - 107d - 108e = 0 (5)
Теперь (4) делим на -1, а (3) делим на 2.
И перепишем уравнения немного в другом порядке:
{ a + b + c + d + e = 0 (1)
{ 0a + b + 2c + 3d + 4e = 0 (4)
{ 0a - 8b - 12c - 14d - 15e = 3 (2)
{ 0a - 27b - 36c - 39d - 40e = 0 (3)
{ 0a - 81b - 102c - 107d - 108e = 0 (5)
Умножаем (4) на 8 и складываем с (2).
Умножаем (4) на 27 и складываем с (3).
Умножаем (4) на 81 и складываем с (5).
{ a + b + c + d + e = 0 (1)
{ 0a + b + 2c + 3d + 4e = 0 (4)
{ 0a + 0b + 4c + 10d + 17e = 3 (2)
{ 0a + 0b + 18c + 42d + 68e = 0 (3)
{ 0a + 0b + 60c + 136d + 216e = 0 (5)
Умножаем (2) на -9, а (3) умножаем на 2:
{ 0a + 0b - 36c - 90d - 153e = -27
{ 0a + 0b + 36c + 84d + 136e = 0
И складываем эти уравнения:
0a + 0b + 0c - 6d - 17e = -27 (3)
Умножаем (2) на -15, а (5) оставляем, как есть:
{ 0a + 0b - 60c - 150d - 255e = -45 (2)
{ 0a + 0b + 60c + 136d + 216e = 0 (5)
И складываем эти уравнения:
0a + 0b + 0c - 14d - 39e = -45 (5)
Собираем все уравнения обратно в систему и перенумеруем их:
{ a + b + c + d + e = 0 (1)
{ 0a + b + 2c + 3d + 4e = 0 (2)
{ 0a + 0b + 4c + 10d + 17e = 3 (3)
{ 0a + 0b + 0c - 6d - 17e = -27 (4)
{ 0a + 0b + 0c - 14d - 39e = -45 (5)
Последний шаг. Умножаем (4) на -7, а (5) умножаем на 3:
{ a + b + c + d + e = 0 (1)
{ 0a + b + 2c + 3d + 4e = 0 (2)
{ 0a + 0b + 4c + 10d + 17e = 3 (3)
{ 0a + 0b + 0c + 42d + 119e = 189 (4)
{ 0a + 0b + 0c - 42d - 117e = -135 (5)
И складываем (4) и (5):
2e = 54
e = 54/2 = 27
Подставляем в (4):
{ 0a + 0b + 0c - 6d - 17*27 = -27 (4)
-6d = 17*27 - 27 = 432
d = -432/6 = -72
Подставляем в (3):
0a + 0b + 4c + 10(-72) + 17*27 = 3 (3)
4с = 72*10 - 17*27 = 720 - 459 + 3 = 264
c = 264/4 = 66
Подставляем в (2):
0a + b + 2*66 + 3(-72) + 4*27 = 0 (2)
b = -132 + 216 - 108 = -24
Подставляем в (1):
a - 24 + 66 - 72 + 27 = 0 (1)
a = 24 - 66 + 72 - 27 = 3
Итак, мы получили коэффициенты этого многочлена:
P(x) = 3x^4 - 24x^3 + 66x^2 - 72x + 27
И, наконец-то, находим P(4):
P(4) = 3*4^4 - 24*4^3 + 66*4^2 - 72*4 + 27 =
= 3*256 - 24*64 + 66*16 - 288 + 27 =
= 768 - 1536 + 1056 - 288 + 27 = 27
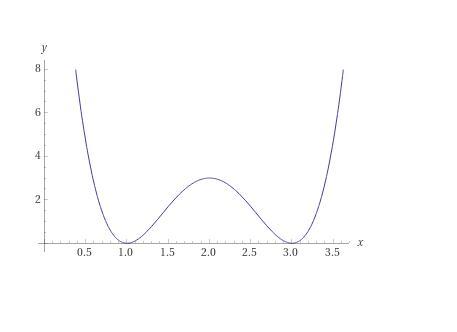
График этого многочлена на рисунке.