Предмет: Математика,
автор: azza234oll45
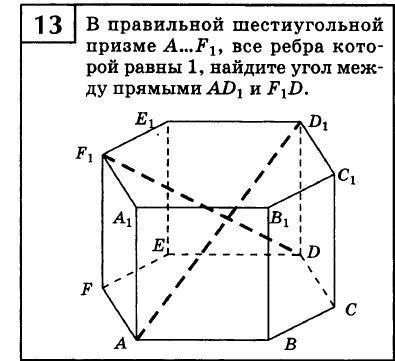
Помогите, пожалуйста, нужно найти угол между прямыми
Приложения:
Ответы
Автор ответа:
1
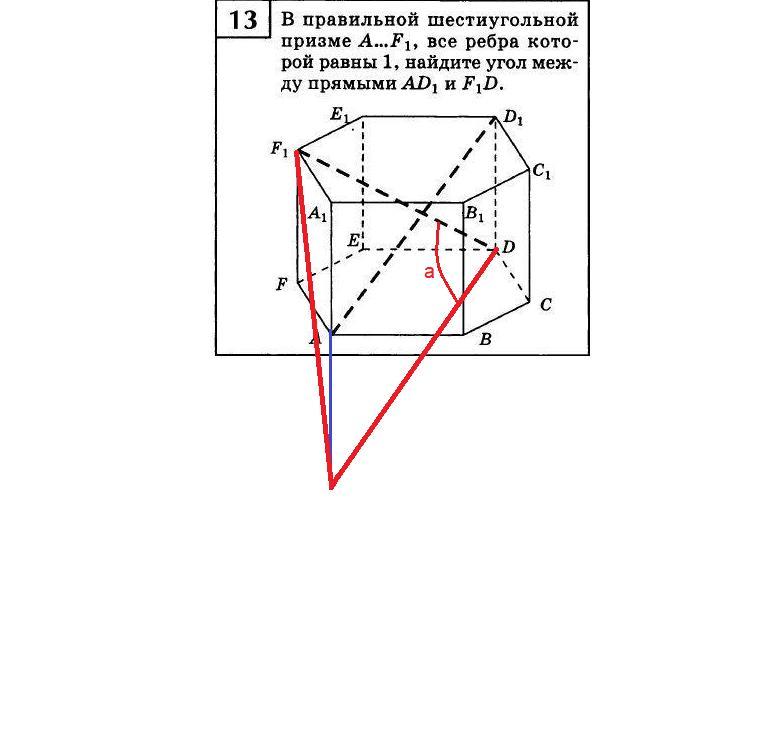
Геометрическое решение.
Применим перенос одного из отрезков так, чтобы их концы соединились.
Перенесём отрезок AD1 точкой D1 в точку D.
При этом точка А перейдёт в точку А2.
Получим треугольник DA2F1 с искомым углом D. Находим длины его сторон.
Сначала определим их проекции на основание.
AD = 1 + 2*(1*cos 60º) = 1 + 2*(1*(1/2)) = 2.
Тогда AD1 = √(2² + 1²) = √(4 + 1) = √5.
Находим DF = 2*(1*cos 30º) = 2*(1*(√3/2)) = √3.
Тогда DF1 = √((√3)² + 1²) = √(3 + 1) = √4 = 2.
И последний отрезок A2F1. Он равен:
A2F1= √(2² + 1²) = √(4 + 1) = √5.
Применим теорему косинусов.
cos D = (2² + (√5)² - (√5)²) / (2*2*√5) = 4/(4*√5) = √5/5 ≈ 0,4472.
Угол D = arccos(√5/5) = 1,1071 радиан или 63,435 градуса.
Приложения:
azza234oll45:
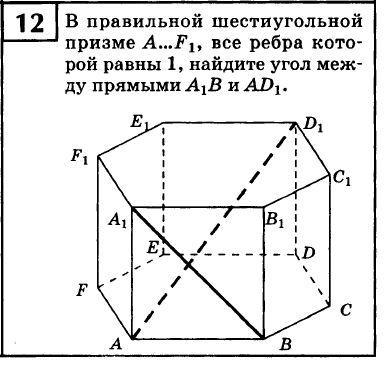
А как на рисунке 12 найти AD1? Можете объяснить, пожалуйства
Для 12 решение аналогично. Отрезок AD1 одинаков, как и в 13. Отрезок А1В лучше перенести точкой В в точку А. Тогда третья сторона будет в верхнем основании. Вычертить шестиугольник и сторону А1В1 удвоить влево. Это будет точка А2 и найти D1A2.
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Другие предметы,
автор: ShadowDencha
Предмет: Окружающий мир,
автор: sglinka
Предмет: Математика,
автор: OtlichnikBEST
Предмет: Физика,
автор: normit662