Предмет: Геометрия,
автор: kateaskripkaru
Допоможіть, срочно....
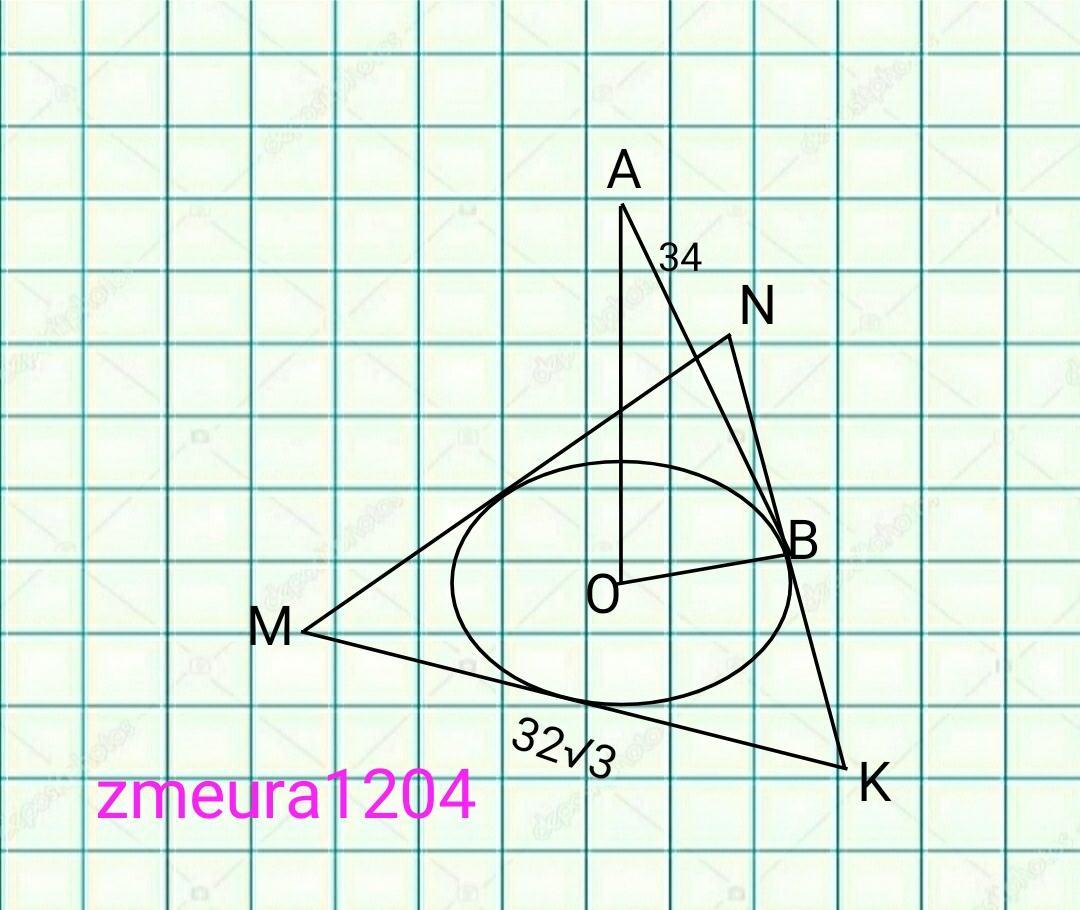
Сторони рівностороннього трикутника дорівнюють 32√3 см. Точка А в просторі дорівнює 34 см від кожної сторони трикутника. Обчисліть відстані від точки А до площини трикутника
Ответы
Автор ответа:
1
Ответ:
30см
Решение:
ОВ- радиус вписанной окружности в равносторонний треугольник ∆МNK.
ОВ=МК/2√3=32√3/2√3=16 см.
∆АОВ- прямоугольный треугольник
По теореме Пифагора
АО²=√(АВ²-ОВ²)=√(34²-16²)=√(1156-256)=
=√900=30см
Приложения:
kateaskripkaru:
Спасибо большое ❤️❤️❤️
Автор ответа:
1
Ответ:
АО=30 см
Объяснение:
точка О центры окружностей описанной и вписанной
сторона многоугольника аn = 2R · sin(π/n) = 2r · tg(π/n) ⇒
r=а/2/ tg(π/3)=32√3/2/√3=16 см радиус вписанной окружности
ОА⊥ к плоскости Δ Из прямоугольного АО=√(34²-16²)=30 см
спасибо большое ❤️❤️
Похожие вопросы
Предмет: Русский язык,
автор: kjjjb
Предмет: Английский язык,
автор: Din1111111
Предмет: Русский язык,
автор: лина350
Предмет: Алгебра,
автор: musical12
Предмет: Литература,
автор: Юылыл