Question

Решите, пожалуйста, срочно! 100 баллов

Answer 1

Ответ:

$1)\ \ s^2-3s+2\geq 0\ \ ,\ \ \ s_1=1\ ,\ s_2=2$

Графиком квадр. трёхчлена является парабола с ветвями, направленными  вверх .

Для нахождения решения надо посмотреть , на каких промежутках ветви параболы выше оси абсцисс ( ось s ) .

Это условие выполняется при  $s\leq 1\ ,\ s\geq 2$  .

$2)\ \ x^2+3,9>0$

Так как  $x^2\geq 0$  для любых действительных значений  х  , то  

$x^2+3,9>0$  верно для любых действительных значений  х , значит  

$x\in R$  .

$3)\ \ 16-x^2>0$

Разложим на множители левую часть неравенства .

$(4-x)(4+x)>0$

Нулями функции, стоящей в левой части неравенства, будут значения  х= -4 и х=4 . Подсчитаем знаки функции в промежутках :

$---(-4)+++(4)---$    .  

Выбираем промежуток, где стоят знаки (+) :   $x\in (-4;\ 4\ )\ .$

$4)\ \ \dfrac{x+31,2}{x-7,8}\geq 0\ \ ,\ \ x\ne 7,8$

Решаем методом интервалов, как в предыдущем примере .

Отметим на оси  х=-31,2  и  х=7,8 . Подсчитаем знаки на

образовавшихся промежутках :  $+++[-31,2\, ]---(7,8)+++$  .

$x\in (-\infty ;-31,2\ ]\cup (\ 7,8\ ;+\infty )$

Answer 2

1. верный ответ 1, т.к. неравенство больше нуля - те значения s, при которых график находится выше оси абсцисс, а равно нулю - те значения s, в которых график касается или пересекается с осью абсцисс. в вашем случае пересекается.

Ответs ≤1 ; s≥2

2. х²+3.9>0 - справедливо для любого х, т.к. х²≥0, 3.9>0, а сумма неотрицательного и положительного чисел есть число положительное, т.е.

Ответ х∈R

3. верный ответ предпоследний, решим неравенство методом интервалов. для чего найдем корни правой части. 16=х²; х=±4

(4-х)(4+х)>0

_______-4__________4_________

-                              +                -

х∈(-4;4)

Ответ (-4;4)

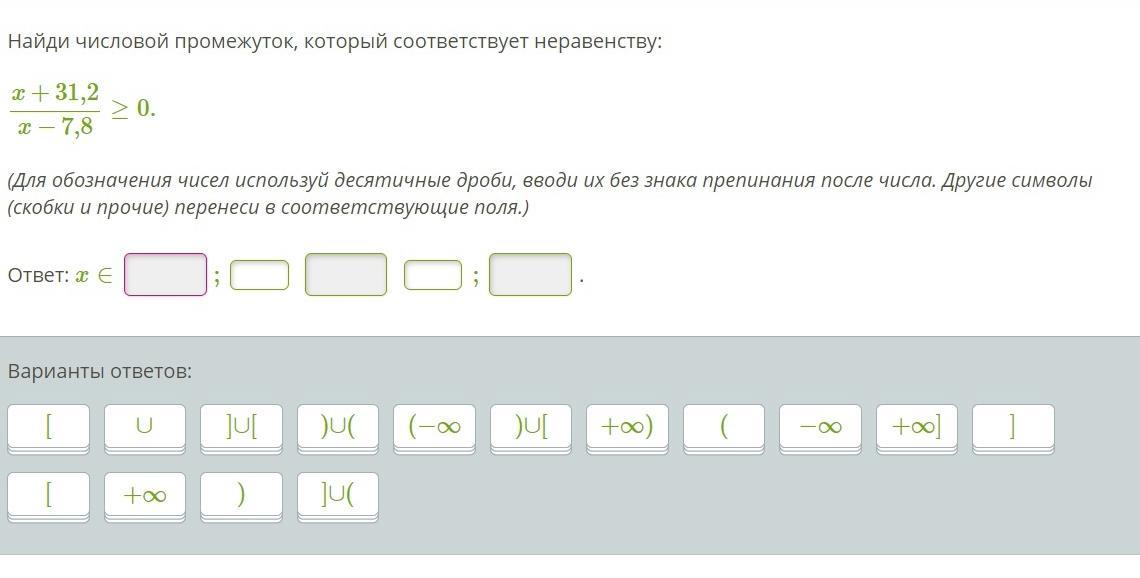
4. данное неравенство равносильно системе

(х+31.2)*(х-7.8)≥0

х-7.8≠0

х+31.2=0⇒х=-31.2

х-7.8=0⇒х=7.8

_______-31.2________7.8__________

 +                        -                      +

х∈(-∞;-31.2}∪(7.8;+∞)