Question

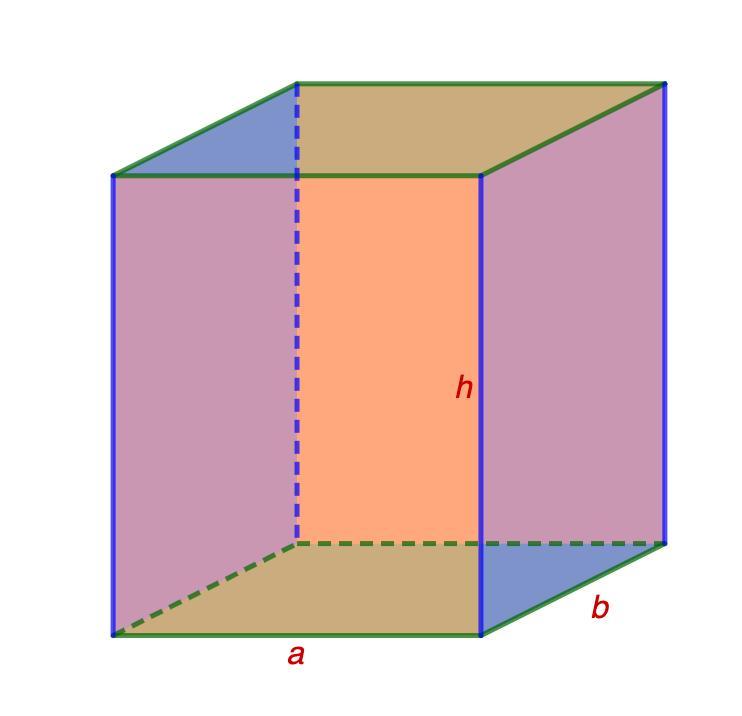
В прямоугольном параллелепипеде площади трёх граней равны 16см в квадрате, 9см в квадрате и 25см в квадрате. Найдите его объём.

Answer 1

Ответ:

Объем параллелепипеда равен 60 см³.

Пошаговое объяснение:

Требуется найти объем прямоугольного параллелепипеда, если известны площади трех граней.

Дано:

S передней грани = 25 см²

S боковой грани  = 16 см²

S нижней грани = 9 см²

Найти: V.

Решение:

Обозначим длину, ширину и высоту параллелепипеда соответственно a, b, h.

• Прямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники.

Вспомним:

• Площадь прямоугольника равна произведению смежных сторон.

1. Рассмотрим данный параллелепипед.

• Объем параллелепипеда равен произведению площади основания на высоту.

• $\displaystyle \boxed { V=S\;_{OCH} *h}$

Основание - это нижняя грань.

Значит площадь основания 9 см².

Теперь найдем высоту.

2. Из формулы площади передней грани выразим a:

S пг = аh        

25 = аh

$\displaystyle \boxed { a=\frac{25}{h} }$

3. Из формулы площади боковой грани выразим b:

S бг = bh        

16 = bh

$\displaystyle \boxed { b=\frac{16}{h} }$

4. В формулу площади нижней грани подставим выше найденные значения а и b и найдем h:

S нг = аb

9 = ab

$\displaystyle 9=\frac{25}{h}*\frac{16}{h}\\ \\ 9=\frac{25*16}{h^2}$

Воспользуемся основным свойством пропорции:

• Произведение средних членов равно произведению крайних.

$\displaystyle 9h^2=25*16\\\\\displaystyle h^2=\frac{25*16}{9}\\ \\h=\frac{5*4}{3} \\\\h=\frac{20}{3}\;_{(CM)}$

5. Найдем объем параллелерипеда.

$\displaystyle V=9*\frac{20}{3}=60\;_{(CM^3)}$

Объем параллелепипеда равен 60 см³.