Предмет: Математика,
автор: abulovao
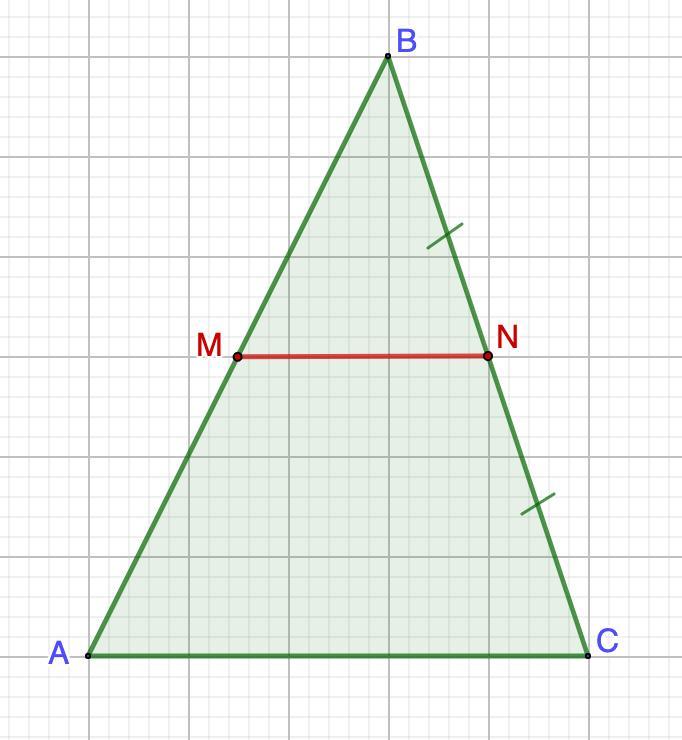
точка N-середина BC.Проведём через нее прямую паралельную в стороне АC.Пусть она пересекает AB
в точке М.Докажем,что M-середина Ab,а(пропуск) -средняя линия треугольника.
Ответы
Автор ответа:
8
Ответ:
То, что точка М - середина АВ, доказано.
Пошаговое объяснение:
Требуется доказать, что точка М - середина отрезка АВ.
Дано: ΔАВС.
BN = NC;
MN || AC.
Доказать: АМ = МВ
Доказательство:
1. Для доказательства воспользуемся теоремой Фалеса:
- Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки отрезки.
По условию:
BN = NC;
MN || AC.
Следовательно, АМ = МВ.
2. Можно воспользоваться признаком средней линии треугольника:
- Если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.
По условию:
BN = NC;
MN || AC.
Следовательно, MN - средняя линия треугольника.
А значит АМ = МВ.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Українська мова,
автор: СатанаМарси
Предмет: Русский язык,
автор: lerageorgieva2
Предмет: Алгебра,
автор: darinatyhonova
Предмет: Математика,
автор: YaRTnT