Предмет: Геометрия,
автор: yes1843
В треугольнике АВС точки М, N. K - середины сторон АВ. ВС, AC. Найди площадь треугольника МИК, если АВ = 10, BC = 13, AC = 13.
Приложения:
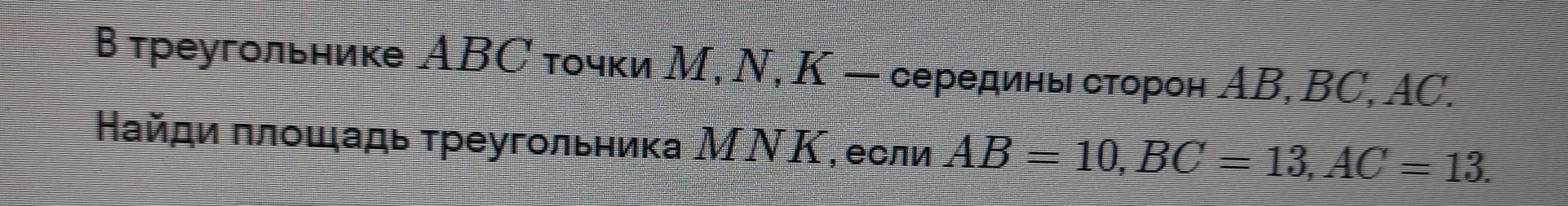
Ответы
Автор ответа:
5
△ABC - равнобедренный (AC=BC), CM - медиана и высота
∠AMC=90°, AM=AB/2=5
CM=√(AC^2-AM^2) =12 (т Пифагора)
S(ABC)= 1/2 AB*CM =60
Или по формуле Герона
p=(a+b+c)/2 =(10+13+13)/2=18
S=√(p(p-a)(p-b)(p-c)) =√(18*8*5*5)=60
Стороны △MNK являются средними линиями △ABC, следовательно параллельны сторонам △ABC и равны их половинам.
△MNK~△ABC (стороны параллельны), k=MN/AC=1/2
Площади подобных фигур относятся как квадрат коэффициента подобия.
S(MNK)/S(ABC) =(1/2)^2 =1/4 => S(MNK)=60/4 =15
Приложения:
siestarjoki:
сорян, при записи подобия вершины должны соответствовать: △MNK~△СAB
спасибо
Похожие вопросы
Предмет: Русский язык,
автор: Olyajkllkkhgfvn
Предмет: Русский язык,
автор: Нарминка1
Предмет: Английский язык,
автор: Oxgdngfmcgndfhmdnhf
Предмет: Русский язык,
автор: artur211022
Предмет: Алгебра,
автор: NoviChok227