Question

Очень срочно! Пожалуйста! Задача С1! Найдите значение наибольшее и наименьшее

Answer 1

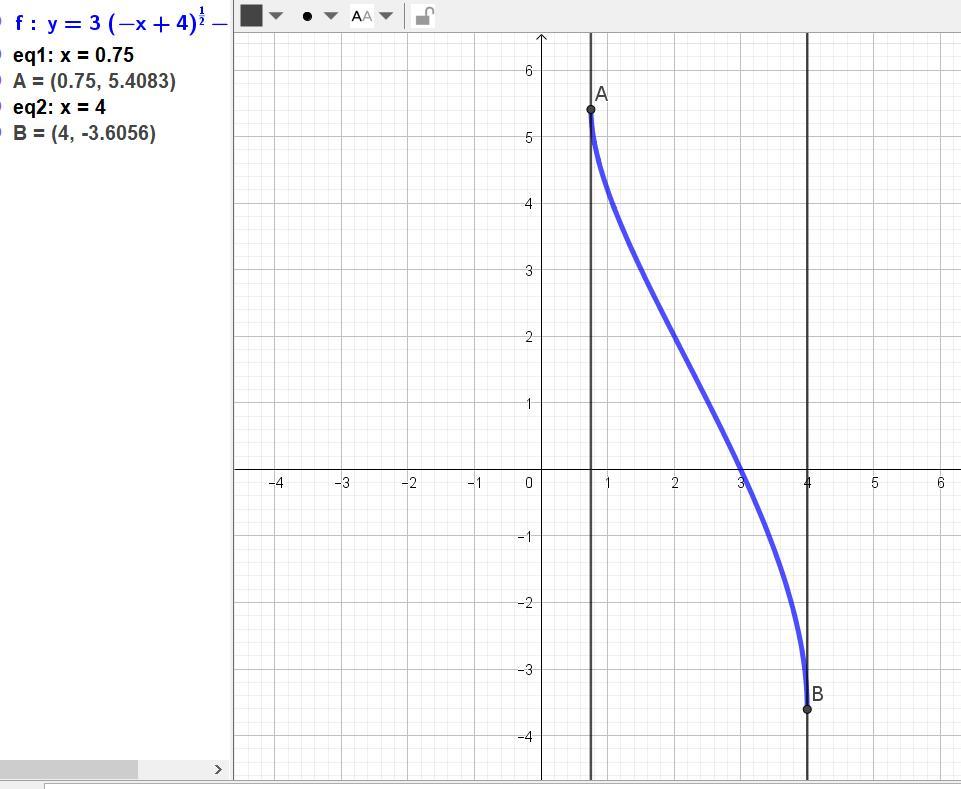
Дана функция y = 3√(-x + 4) - √(4x – 3).

Область её определения – нули или положительные значения подкоренных выражений.

-x + 4 ≥ 0, отсюда х ≤ 4,

4x - 3 ≥ 0, отсюда х ≥ (3/4).

Производная этой функции равна:

y’ = (-2/√(4x – 3)) – (3/(2√(-x+4))).

Как видим, функция убывающая – при положительных знаменателях числители отрицательны.

Поэтому, хотя производная функции не может быть равна нулю, она имеет

максимальное значение при минимальной абсциссе  и минимальное – при максимальной абсциссе.

y(max) = 3√(-(3/4) + 4) - √(4(3/4) – 3) = 3√(13/4) – 0 = (3/2)√13.

y(min) = 3√(-4 + 4) - √(4*4) – 3) = 3*0 – √13 = -√13.