Предмет: Алгебра,
автор: yur4ik15ap490u1
Помогите пожалуйста,нужно упростить выражение даю всё балы что есть
Приложения:
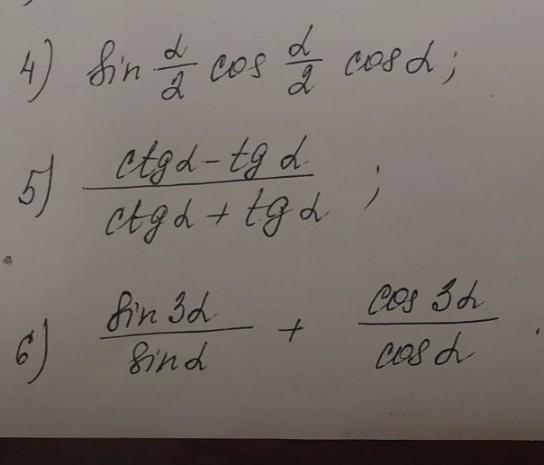
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: RenyaTalacheva
Предмет: Русский язык,
автор: Вилаят
Предмет: Русский язык,
автор: оксимирон228
Предмет: Українська мова,
автор: anastasiiavasylko
Предмет: Математика,
автор: z12316