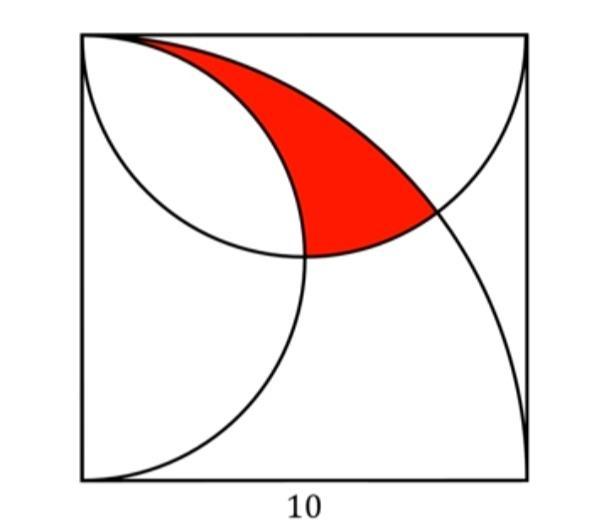
Найти площадь красной фигуры. Если сторона квадрата равна 10.
Ответы
Ответ:
Искомая площадь равна (11π - 25)см² ≈ 8 см² (при π = 3).
Объяснение:
Привяжем систему координат к вершине А данного квадрата АВСD.
Обозначим все точки пересечения c известными координатами на рисунке:
A(0;0), B(0;10), C(10;10), D(10;0) H(5;10), O(5;5).
Найдем координаты точек пересечения двух окружностей с центрами в точках А(0;0) и Н((5;10) и радиусами
R1 = 10 и R2 = 5 соответственно.
Для этого решим систему двух уравнений этих окружностей:
x² + y² = 100 (1) и (x-5)² + (y-10) = 25 (2).
Из (2) имеем: x²-10x+25 +y²-20y+100 = 25.
Учитывая, что x² + y² = 100, получим:
200-10x-20y = 0 или 20-x - 2y = 0. => x = 20 - 2y.(3)
Подставив (3) в (1), получим квадратное уравнение:
5y² - 80y + 300 = 0, решая которое получим:
y1 = 6, y2 = 10 и соответственно х1 = 8 и х2 = 0. То есть точки пересечения с координатами (8;6) и (0;10). Заметим, что вторая точка соответствует точке В, значит первая точка - это точка Е(8;6). Тогда точка F(8;0).
Зная координаты всех точек, имеем:
AG = 5ед, GO = 5ед, OE = √10ед, EF = 6ед.
Теперь найдем необходимые площади.
Площадь фигуры АОВED равна разности площади четверти круга с центром в точке А (радиуса 10) и половины круга с центром в точке J (радиуса 5): Saobed = 25π - 12,5π = 12,5π ед². Из этой площади нам надо вычесть:
1.Площадь Sago, равную разности площади квадрата AGOJ и 1/4 площади круга с центром в точке J радиуса 5.
2.Площадь трапеции GOEF (за вычетом площади сегмента ОЕ круга с центром в точке Н радиуса 5.
3.Площадь половины сегмента круга с центром в точке А радиуса 10 - Sdef.
Итак,
1. Вычитаемая площадь равна:
5·5 - (1/4)·π·25 = (25 - 6,25π) ед².
2. Площадь трапеции
Sgoef = (GO+FE)·GF/2 = (5+6)·3/2 = 16,5 ед².
По длине хорды ОЕ и радиусу R=5 найдем угол ОНЕ (формула): α = 2arcsin(ОЕ/2R)
α = 2arcsin(√(9+1)/10) ≈ 36,8°.Площадь сегмента найдем по формуле:
Sое = (R²/2)·(π·α/180 - sinα), где R = 5, α = 36,8°.
Тогда площадь сегмента равна
Sао = (25/2)·(0,2·π - 0,6) = (2,5π - 7,5) ед².
Вычитаемая площадь равна
16,5 - (2,5π - 7,5) = (24-2,5π) ед².
3. Найдем угол сегмента EDE1 с длиной хорды ЕЕ1=12 и радиуса 10:
α = 2arcsin(12)/20) ≈ 73,7°.
Тогда площадь половины этого сегмента (вычитаемая площадь) равна
Sdef = (1/2)·(R²/2)·(π·73,7/180 - sin(73,7)) = 25·(π·0,41 - 0,96) = (10,25·π - 24) ед².
Найдем искомую площадь:
S = 12,5π - (25 - 6,25π) - (24-2,5π) - (10,25·π - 24) = 11π - 25 ед².
Ответ: площадь красной фигуры равна: S = 11π - 25 ≈ 8 ед² (при π = 3).
P.S. Более точно найти нужные углы можно через вектора. Например, для ∠ОНЕ:
Вектор НО{0;-5}, вектор HE{3;-4}, |HO| = √25 = 5, |HE| = 5.
Cos(∠OHE) = НО·НЕ/(|HO|·|HE|) = (0+20)/25 = 0,8 =>
∠OHE ≈ 36,9°. (разница с формулой в решении 0,1).
Для 2·∠EAD: вектор АЕ{8;6}, вектор АЕ1{8;-6},
|AE| = |AE1| = 10.
Cosβ =(64 - 36)/100 = 0,28 => β = 73,7°. (совпадает).
